| Resumen electrónico de EIR, Vol.XXIV, núm. 7 |
|
|
Estudios estratégicos
por Jason Ross, miembro del LYM Es más, no es menos falso que el centro del mundo esté al interior de la Tierra a que lo esté fuera de ella; ni la Tierra ni ningún otro orbe tiene siquiera un centro. Puesto que el centro es un punto equidistante de la circunferencia, y como no puede haber una esfera o un círculo tan completamente verdadero que no pueda darse por cierto uno que lo sea más, es obvio que no puede afirmarse un centro [que sea tan verdadero y preciso] que no pueda afirmarse uno aun más verdadero y más preciso. La equidistancia precisa de cosas diferentes no puede encontrarse sino en el caso de Dios, porque sólo Dios es Igualdad Infinita. Por tanto, Él que es el centro del mundo, a saber, el Dios Bendito, es también el centro de la Tierra, de todos los orbes y de todas las cosas del mundo. De igual manera, Él es la circunferencia infinita de todas las cosas. En la segunda parte de su Nueva astronomía, Johannes Kepler aborda el movimiento de Marte, tras identificar dos supuestos axiomáticos a priori que habían acotado las investigaciones astronómicas hasta entonces: que los planetas se mueven en círculos perfectos, y que puede encontrarse un punto ecuante para la órbita —un punto desde el cual pueda observarse que el planeta se mueve a una velocidad constante, recorriendo ángulos iguales en tiempos iguales—, un punto de uniformidad. En vez de seguir este enfoque de investigar el movimiento al parecer irregular de Marte, Kepler, con una mente más sana, planteó la pregunta: ¿Cuáles son las características de cambio del movimiento aparente de Marte?[1] 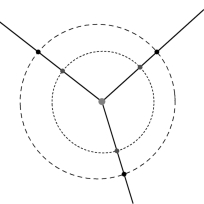 Los planetas que zurcan los cielos sufren una desigualdad de movimiento a causa de la posición cambiante de nuestra Tierra desde donde los observamos. Esta desigualdad puede eliminarse seleccionando ciertas observaciones de los planetas: las que están en oposición, donde su posición es la misma ya sea que se les observe desde el Sol o desde la Tierra (de izq. a der.: Sol, Posiciones de Marte, Sol) Kepler elimina el efecto que surte la Tierra sobre la posición percibida de Marte al usar observaciones en oposición. De este modo, Kepler puede “observar” a Marte desde un punto fijo, el Sol. Y aun en este movimiento de Marte observado desde el Sol subsiste una desigualdad: Marte tiene una posición en relación con el Zodíaco en la que alcanza la mayor velocidad, y otra en la que dismimnuye a la menor. 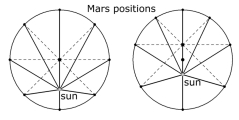 Esta figura muestra dos métodos para explicar este movimiento iirregular, el excéntrico y el ecuante. En el modelo excéntrico (izq.), donde el punto de movimiento uniforme es el centro de la órbita, el observador fuera del centro percibe una velocidad cambiante en el planeta. El modelo ecuante (der.) tiene dos “centros”, uno de movimiento (el ecuante, de arriba) alrededor del cual el planeta recorre ángulos iguales en tiempos iguales, y uno de órbita (al centro), desde el cual el planeta mantiene una distancia constante mientras lo ve el observador (desde el Sol para Copérnico y desde la Tierra para Ptolomeo). Ambos modelos causan un cambio aparente en la velocidad del planeta, como se percibiría desde el Sol, pero a ritmos diferentes. Ptolomeo echa mano del ecuante porque encontró que representa mejor el movimiento de los planetas superiores.[2] Desde Ptolomeo hasta Kepler, la comunidad científica no se atrevió a cuestionar la idea del movimiento uniforme, el supuesto axiomático a priori de que hay una característica de uniformidad inherente al universo, tanto como tampoco la actual fe casi religiosa en la segunda ley de la termodinámica. Kepler, a quien Tico Brahe le encomendó calcular el movimiento del planeta Marte, tenía a su disposición 12 observaciones de oposición cuando escribió la Nueva astronomía. Al seleccionar 4 de estas observaciones, pudo sacar a relucir una ironía. 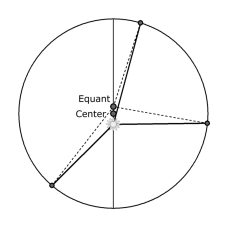 La distancia aparente en el cielo entre la ubicación de Marte en dos oposiciones diferentes indica el ángulo entre esas dos posiciones reales de Marte vistas desde el Sol. El tiempo entre las oposiciones indica el ángulo entre las posiciones de Marte vistas desde el ecuante. Con cuatro de tales observaciones, Kepler siguió un proceso difícil que exigió mucho tiempo, para componer el modelo más preciso jamás creado para predecir la ubicación de Marte en el Zodíaco; él la llamó su hipótesis sustituta. Los tres puntos sobre la línea de los ápsides (la línea que conecta las ubicaciones del movimiento más rápido y el más lento) son, empezando desde arriba, el ecuante, el centro y el Sol. La excentricidad —la distancia del Sol al centro— representa 11,3% del radio de la órbita. Al trazar líneas desde el ecuante que corresponden a los tiempos de las 12 oposiciones, y comparar la ubicación hipotetizada de Marte con la que observó en realidad, Kepler encontró que el margen de error de su modelo estaba dentro de los límites de lo observable.[3] Si cualquier error posible es demasiado pequeño como para percibirlo, ¿significa que ha encontrado la verdad? Otra manera de determinar la excentricidad Entonces Kepler decidió verificar esta excentricidad, al usar mediciones, no de longitud a lo largo del Zodíaco, sino de latitud al norte o el sur del mismo (de izq. de der.: Marte, Tierra, Sol, Centro de la órbita de Marte, Tierra, Marte) 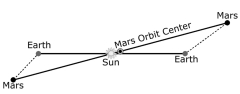 Al observar la latitud de Marte al norte y al sur del plano de la Eclíptica —el plano del movimiento de la Tierra alrededor del Sol—, y usar algo de trigonometría, Kepler pudo determinar qué tan alejado está Marte del Sol en sus límites. La media de estas dos distancias le permitió determinar la ubicación del centro de la órbita de Marte y su distancia del Sol, su excentricidad. Pero esta excentricidad (que se determinó que era entre 8,0 y 9,9% del tamaño de la órbita) no cuadraba con la excentricidad determinada mediante la hipótesis sustituta (11,3%). Pero, ¿cómo puede Marte tener una excentricidad al investigarla según la longitud, y otra según la latitud? En un intento por conciliar estas dos excentricidades, Kepler ajustó su hipótesis sustituta para ubicar el centro de la órbita a medio camino entre el ecuante y el Sol (a esto se le conoce como bisecar la excentricidad). Así, aplicó la excentricidad que determinan las latitudes al modelo funcionalmente perfecto de la hipótesis sustituta. 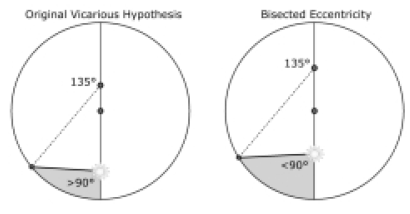
En este diagrama con una excentricidad muy exagerada, la posición percibida de Marte vista desde el Sol cambia al bisecar la excentricidad (hipótesis sustituta original izq., excentricidad bisecada, der.). El ángulo entre Marte y la línea de los ápsides es mayor que 90° en la hipótesis sustituta sin bisecar, y menor que 90° en la versión bisecada. La perfección de la hipótesis sustituta se pierde al introducirse la excentricidad que determinan las latitudes. Al trazar líneas desde el ecuante a ángulos determinados por los tiempos de oposición, Kepler topa con una brecha: este modelo se desvía 8 minutos de arco para la oposición de 1582, un hueco que los sentidos no pueden ver con pasividad, sino que la mente experimenta de un modo activo, creativo. Kepler escribió:[4] Por tanto, algo de entre esas cosas que hemos supuesto tiene que ser falso. Pero lo que se supuso era que la órbita sobre la que se mueve el planeta es un círculo perfecto, y que existe algún punto único sobre la línea de los ápsides a una distancia fija y constante del centro de la excéntrica alrededor del cual Marte describe ángulos iguales en tiempos iguales [el ecuante]. Por consiguiente, de éstas, una o la otra, o quizás ambas, son falsas, puesto que las observaciones empleadas no los son. ¿Cuál es la implicación práctica de esta nueva categoría de experiencia para el dominio del hombre sobre la naturaleza? Kepler, en ese momento, pudo demostrar la existencia necesaria de un principio físico (no geométrico) universal de gravitación. Las implicaciones paradójicas ineludibles del uso del ecuante le impone a la mente una nueva surete de prodigio. Pretender presentar el descubrimiento de Kepler de la gravitación universal sin un análisis cabal de la paradoja del ecuante, equivaldría a darle una respuesta a un público incapaz de formular la pregunta correcta. ________________
|
|
