La geometría del cambio

El autor y algunos miembros del MJL realizando algunos ejercicios pedagógicos. (Houston, Texas)
En su famosa carta a Christiaan Huyghens sobre su descubrimiento de la relevancia de las raíces cuadradas de los números negativos, Godofredo W. Leibniz reconoce claramente que esta investigación se originó con los científicos de la antigua Grecia: "Casi nada más puede desearse del uso que el álgebra puede o podrá tener en la mecánica y en la práctica. Cabe suponer que ésta era la intención de la geometría de los antiguos (al menos la de Apolonio) y el propósito del loci (lugar geométrico—Ndr.) que ha introducido".
Es decisivo entender la implicación de la afirmación de Leibniz para comprender el significado más profundo del tratamiento que Carl F. Gauss le da a El teorema fundamental del álgebra de 1779.
La afirmación de Leibniz desconcertará, o encolerizará al académico moderno, pero tales reacciones sólo son típicas de una enfermedad social más amplia: la incapacidad, como Lyndon LaRouche ha subrayado en repetidas ocasiones, de reconocer la diferencia esencial entre el humano y la bestia. Al igual que cualquier enfermedad, ésta se propaga a través de agentes infecciosos que atacan las defensas de la víctima, haciendo que el propio sistema de la víctima actúe como un agente agresor. La cura para semejantes condiciones consiste en fortalecer las inmunidades naturales de la población amenazada, permitiéndole, no sólo combatir la enfermedad, sino desarrollar una resistencia permanente a sus efectos. En este caso, esas inmunidades naturales son los poderes cognoscitivos de la mente humana. De ahí los efectos terapéuticos de los ejercicios pedagógicos y del arte clásico.
Lo que Leibniz, Gauss y sus predecesores de la antigüedad entendieron, es que la distinción esencial entre el hombre y el animal es la capacidad de la mente humana de ir mas allá del dominio de los sentidos, para descubrir ahí aquellos principios invisibles que gobiernan los cambios percibidos en el universo físico. Sin embargo, al ser invisibles, esos principios sólo pueden descubrirse mediante cambios (movimientos) en el dominio de los sentidos. Éste, a su vez, da paso a paradojas acerca de la relación entre lo visible y lo invisible. En consecuencia, lo que hay que comprender es la interacción aparejada entre lo visible y lo invisible. El movimiento físico da lugar al movimiento voluntario (la pasión) de la mente, de un estado dado a otro superior.
Como indica Leibniz, ningún sistema formal —como el álgebra o la geometría euclidiana— puede representar esta característica de cambio que nace de la interacción entre lo visible y lo invisible.[1] Sólo una geometría del cambio, como la "esférica" preeuclidiana de Tales y la escuela pitagórica, la geometría del movimiento asociada con Arquímedes, Eratóstenes y Apolonio, con el cálculo infinitesimal de Leibniz, o con el concepto de Gauss del dominio complejo, tiene semejante poder.
Al igual que los orígenes del descubrimiento del dominio complejo, también las raíces de sus adversarios se remontan a las culturas mediterráneas antiguas de Egipto y Grecia. El método de ataque ha sido el de inducir a la falsa creencia de que los mundos físico visible e inmaterial invisible no interactúan, sino que están herméticamente separados. Esta creencia es típica de las sectas misteriosas de las antiguas culturas persa y babilónica. Los eleáticos (tales como Parménides y Zenón) pretendían introducir esta perversión en la cultura griega, en contra de Heráclito y los pitagóricos, insistiendo que el cambio es sólo una ilusión y no existe.[2]
Sócrates vs. los sofistas
Sócrates hizo picadillo el argumento eleático de Parménides, así que, después de eso, aquéllos a los que ahora llamaríamos satánicos cambiaron de táctica, expresando la misma intención perversa en la forma de sofismas, tales como admitir que el cambio existe, pero definiendo entonces el cambio, de forma arbitraria, como lo contrario del Bien, y definiendo el Bien como aquello que no cambia y no es corrompido por el cambio.
Sin embargo, luego de que Platón desacreditó los trucos del sofismo, Aristóteles propuso el mismo mal en una nueva guisa, al tiempo que se distanciaba formalmente de los sofistas. Por ejemplo, en su Ética a Nicómaco Aristóteles dice:
"Por esto Dios siempre goza de un mismo y sencillo deleite, porque no solamente el deleite es ejercicio de movimiento, pero aun también de quietud, y aun más consiste el deleite en quietud que en movimiento. Pero la mudanza de todas las cosas, como dice el poeta, es una cosa muy aplacible, por cierta imperfición y falta de natura. Porque así como el hombre malo es fácil de mudar de un parecer a otro, así también es mala naturaleza aquella que tiene necesidad de trastocarse, porque ni es sencilla, ni moderada en su bondad". (
Aristóteles adoptó esta misma perspectiva hacia el movimiento físico, afirmando, en su Física y metafísica, que el movimiento se origina sólo dentro de un cuerpo, y que el movimiento irregular, por implicar más cambio, es de un grado menor que el movimiento regular, el cual es de un grado menor que el estado de reposo.
Al igual que los sofistas y los eleáticos, Aristóteles no estaba desarrollando un argumento original, sino reaccionando contra la reiterada demostración de Platón de que lo material y lo inmaterial van aparejados:
"El origen de este mundo está, en efecto, en la acción simultánea de la necesidad y de la inteligencia. Superior a la necesidad la inteligencia la persuadió dirigiera hacia el bien a la mayor parte de las cosas que nacen y porque la necesidad se dejó persuadir por los consejos de la sabiduría, es por lo que fue primeramente formado el universo". (
Y es el poder de conocer el universo mediante la interacción entre lo visible y lo invisible, entre lo temporal y lo eterno, lo que representa la naturaleza humana. El cambio es una característica, no del vicio y la maldad, sino de la perfección:
"La observación del día y de la noche y las revoluciones de los meses y de los años nos han proporcionado el número, revelado el tiempo e inspirado el deseo de conocer la naturaleza y el mundo. Y así nació la filosofía, el más preciado presente que los dioses le han hecho y podrán hacer jamás a la raza mortal... Dios, al crear la vista y dárnosla, no ha tenido más objeto que ponernos en condiciones, después de que hayamos contemplado en el cielo las revoluciones de la inteligencia, de sacar partido de ellas para las revoluciones de nuestro propio pensamiento, las cuales, por desordenadas que sean, son de la misma naturaleza que las primeras por bien ordenadas que sean, a fin de que instruidos por este espectáculo y tomando parte de la rectitud natural de la razón aprendamos, imitando los movimientos perfectamente regulares de la divinidad, a corregir la irregularidad de los nuestros.
"La misma observación referente a la voz y al oído y por las mismas razones no los donaron los dioses... Y si la voz tiene la facultad de apoderarse de los sonidos musicales, cuya importancia es incontestable, es a causa de la armonía, y ésta, cuyos movimientos son semejantes a los de nuestra alma, al que cultiva con inteligencia el comercio con las musas no le parece que tenga más destino que el de procurarnos frívolos placeres, los solos que se le piden hoy día; al dárnosla, las musas han querido ayudarnos a reglar y a poner de acuerdo entre sí a las caprichosas revoluciones de nuestra alma. Y nos han dado igualmente el ritmo como un medio de reformar las maneras desprovistas de mesura y de gracia que se observan en la mayoría de los hombres". (
La tensión en esta ironía socrática, de los principios inmutables del cambio, es el medio por el cual el hombre, y el universo entero, se autoperfeccionan. Como Kepler nota en su Nueva astronomía, es la tensión del descubrimiento de que las órbitas planetarias no son circulares el "que da lugar a un poderoso sentido de maravilla, el cual a la larga lleva a los hombres a buscar las causas".
Quita esa tensión, como hacen Aristóteles, Leonhard Euler, Louis de Lagrange, etc., y extirparás del hombre su naturaleza humana, dejándolo indefenso contra aquellas fuerzas oligárquicas que pretenden esclavizarlo.
La raíz cuadrada de -1 y el movimiento
Aparte del problema del desapasionado (o más probablemente enfurecido) aristotélico de corazón, surge una dificultad persistente para aquellos que quieren comprender el descubrimiento de Gauss del dominio complejo. La dificultad estriba en entender la importancia física de la raíz cuadrada de -1. Para Euler, Lagrange, y Jean le Rond d'Alembert la raíz cuadrada de -1 es sólo una definición desapasionada de la solución a la ecuación x2+1=0. Toda la tensión asociada con su existencia desaparece con la afirmación de que es una definición de algo que es "imposible". ¿Para qué me preocupo de algo que es imposible?
La dificultad para la persona seria que busca asimilar la idea de la raíz cuadrada de -1, surge del hábito obstinado de empezar con un conjunto de axiomas, postulados y definiciones que son indiferentes al universo físico, para llegar, mediante una serie de pasos lógicos, a la raíz cuadrada de -1, y de allí buscar algún significado físico de este número lógicamente definido.
Todos estos esfuerzos son, como suele decir LaRouche, "como tratar de ordeñar un cabrón, y agarrar el producto con un cedazo".
Gauss recalcó que la raíz cuadrada de -1 implica un principio físico, uno que, dijo, "tiene las implicaciones más profundas para la metafísica de la teoría del espacio". Un estudio de los primeros borradores de Gauss revela que su desarrollo del dominio complejo vino de las paradojas del "problema de Kepler", mismas que seguían irresueltas en el cálculo infinitesimal de Leibniz. Con eso en mente, junto con lo arriba dicho, el significado físico de la raíz cuadrada de -1 puede demostrarse, como indicó Leibniz, conceptualizando la sucesión unificada de descubrimientos desde Pitágoras hasta Gauss. Es sólo mediante este enfoque irónico, polifónico, que puede vislumbrarse la importancia física de la raíz cuadrada de -1.
Esto puede hacerse de forma bastante eficiente si uno ha dominado los principios generales expresados en los descubrimientos de doblar el cuadrado y el cubo, y de la catenaria.
Deja a un lado toda noción algebraica formal, junto con aquellas nociones fijas de corte euclidiano de la geometría. Mira estos descubrimientos desde la perspectiva del movimiento.
El descubrimiento de que al cuadrado lo dobla (o lo parte en dos) un principio diferente que una línea, queda de manifiesto en la determinación de Pitágoras de la inconmensurabilidad entre el lado de un cuadrado de área 1 y el lado de un cuadrado de área 2. Esta relación determina un nuevo tipo de magnitud, el cual, al igual que todos los números, no es susceptible de definición formal fuera de la relación física que la origina. En otras palabras, la raíz cuadrada de 2 no es el número 1,14142135..., sino una magnitud que sólo existe en la relación física de dos cuadrados cuyas áreas tienen una proporción de 1:2.
Platón relata en el
No obstante, a toda esta clase de magnitudes no puede generarla más que un tipo de movimiento físico, la acción circular.
Sin embargo, al doblar el cubo surge un tipo enteramente nuevo de magnitudes. Como afirma Platón en el
Del modo que la construcción de Arquitas lo demuestra, este nuevo tipo de magnitud no puede generarse por la acción circular, sino que requiere una acción circular actuando de forma ortogonal sobre otra acción circular. Esta acción sobre la acción es la que genera el toro, el cilindro y el cono de la famosa construcción de Arquitas. Más tarde, Menecmo y Apolonio demostraron la forma más general del principio de la construcción de Arquitas mediante el desarrollo de las secciones cónicas. Para ellos, así como para Arquímedes, Eratóstenes y demás, era esta forma superior de acción física, expresada por el movimiento que actúa sobre el movimiento, la que generaba las relaciones que se manifiestan en los cuerpos sólidos, tales como los cuadrados y los cubos. A diferencia de lo que Aristóteles afirma, el movimiento no se origina en los cuerpos. Los cuerpos tienen su origen en el movimiento
Para recapitular: las magnitudes asociadas con una media geométrica entre dos extremos son de una especie generada por un principio de movimiento, es decir, por la acción circular, y las magnitudes asociadas con dos medias geométricas son de una especie generada por otra clase de movimiento, es decir, por la acción cónica.
La 'clase de clases'
Sin embargo, como Leibniz y Jean Bernoulli indicaron, esta última forma de movimiento (cónico) en realidad genera una clase de clases de magnitudes. Cada clase separada se caracteriza por el número de medias entre dos extremos, y se identifica con un tipo específico de poder (por ejemplo, el cuarto poder requiere tres medias geométricas entre dos extremos, el quinto poder implica cuatro medias geométricas, etc.).[6]
Leibniz llamó a tales magnitudes "algebraicas" o "poderes algebraicos". A las magnitudes asociadas con la clase de clases superior, Leibniz las llamó "trascendentales". Estas magnitudes trascendentales existen fuera del dominio de lo algebraico. No obstante, ambas están conectadas, porque las trascendentales superiores generan a las algebraicas inferiores. Como establece Leibniz, las trascendentales son las que expresan las relaciones que surgen en el universo físico.
La importancia física de las dos primeras clases de poderes algebraicos, los cuadrados y los cubos, es evidente en los problemas de Pitágoras y Arquitas. ¿Cuál es la importancia física del movimiento que genera la clase entera de poderes algebraicos? Ésta radica en la solución de Leibniz al problema de la catenaria. En tanto expresión del principio de acción mínima, la catenaria es la forma que cobra una cadena suspendida que está inmóvil. Pero, como Leibniz demuestra, la inmovilidad de la cadena refleja el movimiento que generan las magnitudes trascendentales superiores. En el caso de la catenaria, ese movimiento se expresa como dos curvas exponenciales (ver figura 1).
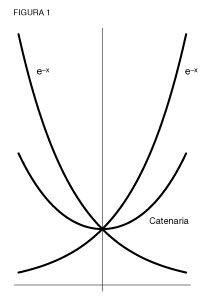
La catenaria visible, indica Leibniz, es la media aritmética entre dos curvas exponenciales. Pero esa es sólo la mitad de la historia. Parafraseando a Platón en el
Podemos darnos una idea viendo las otras expresiones de la relación exponencial, como la hipérbola y la espiral logarítmica. En los tres casos existen dos formas distintas, la izquierda y la derecha (ver figuras 2a y 2b). Estas dos formas no pueden transformarse la una en la otra dentro del plano de su existencia visible.
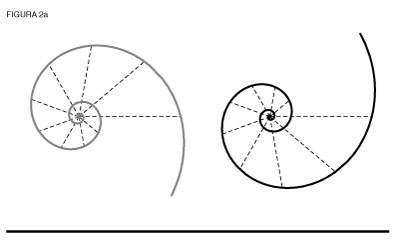
Pero, como demuestra la catenaria, el universo físico sólo está contento cuando ambas formas se unen en una. ¿Cuál es la naturaleza de las especies de movimiento que unen a las exponenciales izquierda y derecha?
Ese movimiento representa una rotación ortogonal del plano visible de las dos curvas (ver figura 3). (Estas figuras sólo tienen el propósito de ilustrar. Te recomiendo que construyas los modelos físicos de este movimiento).
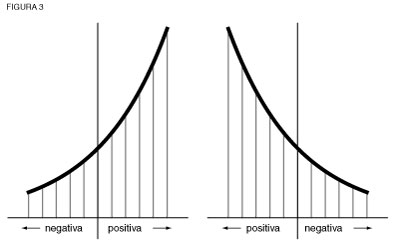
Esta es la acción que Gauss entendió como la acción física que da origen a la raíz cuadrada de -1. Para visualizar esto, mira una de las exponenciales.
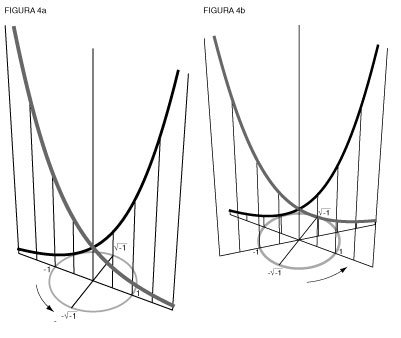
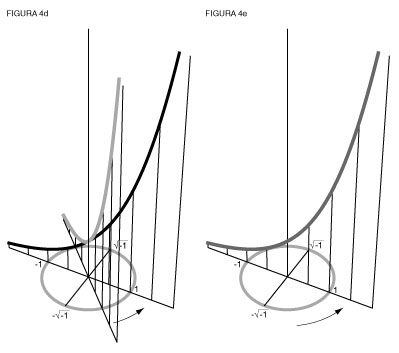
La misma genera todos los poderes algebraicos, creciendo en una dirección y decreciendo en la otra (ver figuras 4a, 4b, 4c, 4d y 4e).Ahora ve la otra exponencial.

Hace lo mismo, pero en la dirección en que una crece, la otra decrece, y viceversa. Desde este punto de vista, ambas son mutuamente excluyentes.
No obstante, la catenaria las une. Si llamamos, como hizo Gauss, a una exponencial positiva y a la otra negativa, entonces las dos están unidas por la media geométrica entre 1 y -1, o la raíz cuadrada de -1.
¿Existe físicamente la raíz cuadrada de -1? Sólo pregúntale a la catenaria.
¿Puede verse?
Sí, pero sólo por los humanos. No por los animales ni por los aristotélicos.
____________________
__________________________________________________
—Traducción de Manuel Hidalgo.
NOTAS:
[1] Luego de que Leonhard Euler —el ideólogo que aborrecía a Leibniz— y su protegido Lagrange publicaron sus ataques fraudulentos contra Leibniz por este principio decisivo de su definición original del cálculo infinitesimal,
[2] Bertrand Russell y los proponentes actuales de la "teoría de la información" se consideran ellos mismos como seguidores de la tradición de los eleáticos.
[3]
[4]
[5] Ibíd.
[6] Nota del traductor: El problema que enfrentan tanto el traductor como el lector respecto al significado de dúnamis en tanto poder, es conceptual y no semántico. Por ejemplo, en este artículo, escrito originalmente en inglés, el autor optó por la voz inglesa power para vertir el concepto de dúnamis.
En castellano, lo que sucede es que enfrentamos un dilema diferente. Si usáremos la voz potencia, como lo hacen la mayoría de los traductores, el lector moderno traería consigo dos conceptos diferentes y hasta contradictorios de esa palabra: una, probablemente la dominante, es la idea algebraica de un número exponencial, referente al grado, condición o estado existente de una ecuación o relación energética; la otra, es la connotación de poder generador o capacidad para producir cambios.
Para Platón, y para toda la escuela griega clásica de matemáticas, no había ninguna ambigüedad o división conceptual respecto a dúnamis. Significaba un poder generador o poder de construcción ubicado en el dominio de la física, y no en el de las matemáticas. Esta claridad conceptual fue destruyéndose como resultado de la introducción, por parte de Aristóteles, de la basura anticientífica de que la certeza sensorial es la base del conocimiento y que, por tanto, el único dúnamis que puede existir es el que puede verse o tocarse: la potencia.
Es así que, en aras de evitar tal contaminación aristotélica del concepto original platónico, en general hemos traducido dúnamis al castellano como poder, salvo en esos casos específicos donde se refiere a las exponenciales algebraicas como tales.