La larga vida de la catenaria,
de Brunelleschi a LaRouche

Lograr el urgente cambio necesario para pasar de ser una sociedad de consumo a una productora requiere, en lo fundamental, un cambio en la forma de pensar. La mente del consumidor conoce el universo sólo a través de los objetos que estimulan los sentidos, y de los poderes mágicos que cree los controlan. Cuando enfrentan una crisis, como la actual, los consumidores se aterran. Exigen que un sacerdocio de asesores financieros y creadores de opinión cada vez más impotente actúe e, incapaces de aumentar la confianza del consumidor, no consiguen resultados. A medida que la crisis se profundiza, aumentan las sospechas de que las potencias invisibles en las que han confiado, o se quedaron sordas o huyeron de la escena. Sin embargo, su principal error es pensar que tales fuerzas del mercado existieron alguna vez y, así, la idea de su existencia previa persiste y sigue gobernando los pensamientos y las acciones de los consumidores, y alimentando un pesimismo cada vez más desesperanzador.Así eran las cosas en Florencia, Italia, cuando luego del desplome del sistema financiero feudal casi 80% de la población murió por los efectos de la peste negra, entre 1347 y 1350. El poeta florentino Giovanni Boccaccio, en la introducción de su obra El Decamerón, describe las reacciones de la población a esa crisis. Según Boccaccio, sus compatriotas se habían sumido en un estado de austera penitencia, de jarana bacanal, o de alguna otra forma de “preparación para el número uno :

“Así, siempre adhiriendo a su inhumana decisión de esquivar a los enfermos tanto como fuera posible, ordenaron su existencia. En este extremo del sufrimiento y la congoja de nuestra ciudad, la venerable autoridad de las leyes, humanas y divinas, fue humillada, y todas se disolvieron por la ausencia de aquéllos que debían haberlas administrado y hecho cumplir, la mayoría de los cuales, como el resto de los ciudadanos, o estaban sordos o enfermos, o tan acondicionados a ser siervos que eran incapaces de desempeñar ninguna función con la cual cada hombre fuera libre de hacer lo correcto”.

En su intento de rescatar a su ciudad y a la civilización europea de esta tragedia, un grupo de líderes florentinos en la tradición cristiano–platónica de su predecesor, Dante Alighieri, reconoció que el poder de superar tales catástrofes radica, no en el dominio de la certeza sensorial y los poderes mágicos, sino en el poder de la mente humana de descubrir y emplear los principios veraces que gobiernan al universo. Para demostrar ese poder, decidieron terminar la catedral de Santa María de Fiore, cuya construcción había comenzado casi tres cuartos de siglo antes. El plan requería la construcción de un tambor octagonal de un diámetro enorme —42 metros—, que estaría coronado con una cúpula autoestable que se alzaría sobre la ciudad y dominaría todos los alrededores (ver figura 1).

Cuando en 1367 se decidió emprender este proyecto, el hombre que finalmente lo concretaría, Filippo Brunelleschi, ni siquiera nacía todavía; sin embargo, la intención que lo guiaría ya estaba plasmada en el tamaño de la estructura y en los requisitos de su diseño. La cúpula igualaría en tamaño al Panteón romano, ese templo dedicado a los poderes mágicos que habían dominado la opinión popular romana y bajo cuya autoridad los emperadores habían gobernado (ver figura 2).

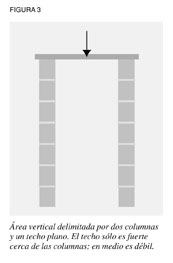
Desde su construcción en 128 d.C., bajo el mandato del emperador Publio Elio Adriano, el Panteón fue la mayor estructura cubierta del mundo, y aunque los emperadores ya no gobernaban en su nombre, la actitud de la cultura romana que simbolizaba persistió en el pensamiento de la población europea, la cual, en una condición bestial, vivía subyugada por el temor a una oligarquía feudal.

La cúpula era un proyecto de un optimismo audaz. A diferencia del Panteón, la cúpula florentina sería bella tanto por dentro como por fuera; una cualidad dirigida a contrarrestar la persistente cultura panteónica que revivió la todavía reciente calamidad de la que Europa aún no se recuperaba. Nunca antes se había abovedado una estructura de tales dimensiones con una cúpula autosostenida y autoestable. Su belleza demostraría un principio compartido por la ciencia y el arte. Como tal, transformaría a toda la región circundante y, a través de los viajeros, al mundo entero.

Los diseñadores originales desconocían las implicaciones de los principios necesarios para construir la cúpula. Para lograr la hazaña, Brunelleschi tendría que descubrir, aplicar y comunicar una forma del principio de acción mínima universal, cuya posterior elaboración vendría en el transcurso de los siguientes 500 años. Este proceso dio un salto en 1988, cuando Lyndon LaRouche visitó la cúpula y reconoció las implicaciones de los descubrimientos de Brunelleschi para los avances posteriores de Godofredo Leibniz, Carl Gauss y Bernhard Riemann, y para el desarrollo futuro de una nueva ciencia física.[1]

La cúpula y la geometría antieuclidiana

Imagínate en 1420 observando el tambor octagonal de Santa María de Fiore, sin la cúpula. ¿Qué ves? ¿Un espacio vacío? Si es así, nunca podrías imaginar, y mucho menos construir la cúpula. La construcción de la cúpula requirió un dominio de principios invisibles al ojo humano. No son los poderes mágicos e invisibles del Panteón, sino los principios físicos universales que, aunque invisibles, se conocen claramente a través de la imaginación. Tanto para el científico como para el artista, no hay tal cosa como un espacio vacío, no existe un óleo vacío, ninguna pizarra en blanco. Lo que existe es una multiplicidad de principios físicos caracterizada por un conjunto de relaciones cuya expresión finalmente adopta la forma de una obra de arte. Para ver la cúpula sin construir, tal como el artista Brunelleschi habría hecho, imagina los principios físicos, y los ladrillos y el mortero cobrarán la forma requerida.

Esta es la base para empezar a construir una geometría física desde la perspectiva de Brunelleschi, Leibniz, Gauss, Riemann y LaRouche. Las raíces de esta geometría física se remontan a los descubrimientos —en la antigua Grecia— de Tales, Pitágoras, Arquitas, Platón, Menecmo, Arquímedes y Eratóstenes, quienes —a diferencia de la exposición de los Elementos de Euclides— derivaron los principios de la geometría de la investigación de los principios físicos, no de nociones abstractas de espacios vacíos.

Desde el asesinato de Arquímedes a manos de soldados romanos en 212 a.C., el pensamiento europeo estuvo dominado por la doctrina de Aristóteles de que los principios universales no tienen efecto sobre los asuntos terrenales, y de que el conocimiento de tales principios es imposible. Por tanto, los seres humanos sólo podían confiar en la percepción sensorial y en las proposiciones de una geometría abstracta derivada, por deducción, de axiomas y opiniones comunes que no pueden comprobarse, los cuales estaban separados del mundo físico, del mismo modo que —según Aristóteles— los cielos estaban separados de la Tierra. Para construir la cúpula, Brunelleschi tuvo que rechazar el aristotelismo y recurrir a la ciencia platónica, la cual entendía que al mundo físico lo gobernaban principios físicos universales, y que, aunque visibles, la mente humana tenía el poder de descubrirlos y usarlos, aumentando así el poder del hombre en y sobre el universo.

Los principios físicos vs. Artistóteles

Para comprender esto, examina algunos problemas simples de la construcción de edificios en los que destaca la distinción entre los principios físicos de la gravitación universal y las nociones aristotélicas de la geometría abstracta. Comienza con una columna vertical, la cual adopta la forma de una línea. Según Euclides, una línea geométrica abstracta es una extensión en un espacio vacío que sólo tiene longitud. No importa cuán larga sea la línea, su anchura es siempre la misma, es decir, cero. Sin embargo, cuando construimos una columna (línea) vertical de ladrillos, entre más alta es la columna mayor es el peso (presión) que ejerce sobre los ladrillos inferiores. Construir una columna más alta requiere fortalecer las porciones inferiores de la columna ensanchando la base, o usando otros métodos tales como apuntalar la columna desde fuera.

Traslada esta idea a un área o superficie. Desde la perspectiva del espacio vacío euclidiano, una superficie es algo que tiene longitud y ancho. Un área circunscrita está delimitada por una línea, ya sea recta o curva. Sin embargo, a un área física la delimita una estructura física cuya forma debe estar determinada por principios físicos. Una propuesta para delimitar un área física sería construir dos columnas verticales y conectar esas columnas con un techo. Pero ésta es una estructura relativamente débil, porque el techo sólo es fuerte cerca de donde se apoya en las columnas. Cuanto más alejadas se encuentran las columnas, mayor la debilidad del techo (ver figura 3).[Un arco es una estructura mucho más estable para albergar un área vertical.

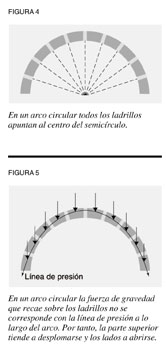
A primera vista, el círculo parece ser la clase más simple de arco, pues el límite circular encierra la mayor superficie en el menor perímetro. Puede construirse un arco circular relativamente estable si el arco está diseñado de forma tal que todos los ladrillos apunten hacia el centro del círculo (ver figura 4).Sin embargo, mientras el arco está en construcción no puede sostenerse por sí mismo y necesita un andamiaje temporal que lo sostenga. Así, el arco entero se autosostiene, pero sus partes no pueden sostenerse por sí solas.

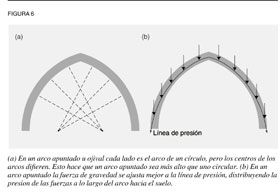
El arco circular presenta otro problema. A pesar de encerrar la mayor superficie en el menor perímetro, su altura es una función de su ancho y la línea de presión no se amolda a la curva circular (ver figura 5).La única forma de encerrar una superficie de mayor altura es ampliando el arco, lo cual, a su vez, disminuye la estabilidad total de la estructura por la presión que ejercen los ladrillos superiores hacia abajo, empujando los lados del arco hacia fuera. Así, aunque desde el punto de vista de la geometría abstracta el círculo es isoperímetro, desde el de la geometría física hay otra forma que proporciona una mayor estabilidad para una superficie mayor. La forma que logra esto es un arco apuntado u ojival, en el cual las dos curvas que lo forman son circulares y tienen distintos centros (ver figura 6a). El arco apuntado, no sólo encierra una superficie mayor, sino que tiene mayor estabilidad porque su curvatura se ajusta más a la línea física de la fuerza en la estructura (ver figura 6b). Así, la forma de un arco en una construcción no la determinan las características de la geometría abstracta, sino las de la geometría física.

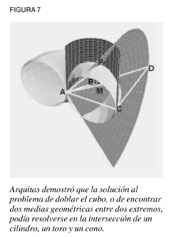
Pero, Brunelleschi tuvo que construir más que un arco, tuvo que encerrar un volumen. En términos geométricos, a un volumen lo encierra un área, la cual se produce al mover una curva. Por ejemplo, en la famosa construcción de Arquitas, cuando se mueve un círculo a lo largo de una línea se produce un cilindro, cuando se rota alrededor de un punto se obtiene un toro, cuando se rota alrededor de una línea se crea una esfera, y cuando se rota un triángulo alrededor de una línea se produce un cono (ver figura 7). De este modo, una cúpula puede formarse rotando un arco, ya sea circular o apuntado, alrededor de un eje (ver figura 8).Pero un área física, como una cúpula, no es sólo la suma de un número infinito de arcos rotados, porque surgen nuevas fuerzas en la cúpula que no existen en ninguno de los arcos. Además de la fuerza a lo largo del arco (que va de arriba a abajo, es decir, que es “longitudinal”), existen fuerzas alrededor de la cúpula (“circunferenciales” o “arqueadas”). El problema que uno enfrenta cuando construye una cúpula radica en determinar qué forma distribuye estas fuerzas diferentes de la mejor manera, según los principios de la gravitación universal.

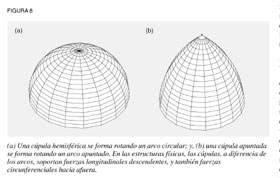
Una solución, la cúpula hemisférica, basada en el arco circular, encierra el mayor volumen dentro de la menor superficie. Pero, al igual que en el arco circular, la altura de la cúpula hemisférica es una función de su ancho. Para poder construir cúpulas más altas, los arquitectos islámicos adaptaron el principio del arco apuntado a la forma de una cúpula apuntada. Al igual que el arco apuntado, la cúpula apuntada no sólo es más alta, sino más estable, pues distribuye las fuerzas en la dirección de la fuerza de gravedad.

No obstante, nadie había construido una cúpula del tamaño de la que Brunelleschi proponía. Por tanto, tuvo que diseñar una estructura cuya forma equilibrara estas fuerzas sin necesidad de apuntalamiento externo, pues minaría la belleza de la cúpula y, así, su eficacia para transformar a la sociedad elevando las mentes de la población.

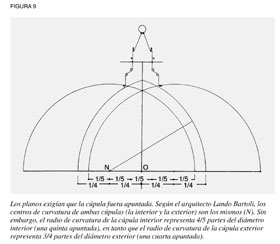
Brunelleschi enfrentó un problema adicional. Una cúpula, al igual que un arco, por lo general necesita un andamiaje de soporte o una cimbra que la sostenga mientras dura su construcción. Aquí, Brunelleschi encaró el obstáculo más formidable. La cúpula propuesta para Santa María de Fiore era tan grande, que excedía la disponibilidad de madera para construir el andamiaje. Brunelleschi sorprendió a sus competidores al proponer construir la cúpula sin ninguna cimbra. Este paso audaz hizo que Brunelleschi diseñara la cúpula de tal forma que, de conjunto y en cada una de sus partes, se autosostuviera. Semejante forma no podía determinarse con los métodos asociados con la geometría euclidiana; la forma que necesitaba Brunelleschi sólo podía determinarse mediante principios físicos.

La construcción de la cúpula

Brunelleschi propuso la construcción de dos cúpulas, una dentro de la otra, con una escalera entre ellas. Ambas se amoldarían al arco apuntado del diseño original. Sin embargo, según el arquitecto moderno Lando Bartoli,[1] la curva de la cúpula interior se basaba en un círculo cuyo diámetro era cuatro quintos del diámetro interno del tambor octagonal (una “quinta apuntada”), en tanto que la curva de la cúpula exterior debía ser tres cuartas partes del diámetro exterior (una “cuarta apuntada”; ver figura 9).

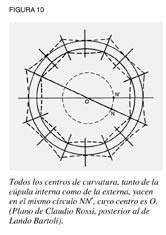
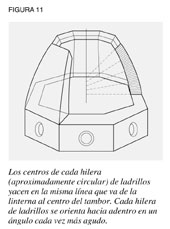
Como tenía que evitar el uso de una cimbra, Brunelleschi tuvo que controlar con mucho cuidado la forma de ambas cúpulas mientras se construían. Ello implicó controlar tres curvaturas diferentes: la longitudinal, la circunferencial y la interior que va hacia el centro de la cúpula. Si las tres curvaturas podían controlarse durante las diferentes fases de construcción, la cúpula no sólo sería estable una vez terminada, sino que cada fase sería lo bastante estable como para servir de plataforma de construcción para la siguiente. Esto significaba que la cúpula tenía que ajustarse a una forma que pudiera autosostenerse tanto de conjunto como en cada una de sus partes.

Cada dirección de curvatura la determinaba otra curvatura. La curvatura longitudinal desde la linterna hasta el tambor estaba definida por el diseño de la quinta y la cuarta apuntada, tal como lo expresan los ocho nervios primarios (blancos) y una serie de nervios intermedios (invisibles, incrustados). Mientras que cada nervio es un arco circular, los centros de la curvatura de cada uno son diferentes; todos los centros yacen a lo largo de dos círculos (uno para la cúpula interna y otro para la externa) dentro de la base del tambor. (ver figura 10). La curvatura circunferencial también era aproximadamente circular, y el diámetro de cada círculo disminuía con la altura. Los centros de curvatura de los círculos yacen en una línea que se extiende desde el centro del tambor hasta la linterna. Asimismo, cada hilera de ladrillos debía torcerse cada vez más hacia adentro a medida que las hileras llegaban a la punta (ver figura 11). Este ángulo tenía que ser uniforme en cualquier hilera, pero debía variar de hilera en hilera en una proporción precisa, pero no uniforme.

Brunelleschi tuvo que resolver un sin fin de problemas, y cada uno de ellos requería nuevas ideas revolucionarias. Pero el descubrimiento central con el que logró tener éxito, el de mayor importancia para el desarrollo futuro de la geometría física antieuclidiana de Kepler, Fermat, Leibniz, Gauss y Riemann, es el que LaRouche identificó: el principio de la catenaria.

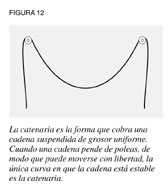
El principio de la catenaria

Una cadena que cuelga libremente cobra una forma única que, al igual que la cúpula de Brunelleschi, se sostiene por sí misma y a cada una de sus partes. Esto puede demostrarse de forma experimental colgando una cadena entre dos poleas que puedan moverse con libertad (ver figura 12). La cadena encontrará sólo una “órbita” o trayectoria estable entre las poleas, pero, una vez que la encuentra, es muy estable. Esta es la característica que LaRouche ha comparado con el principio del “movimiento congelado” de la escultura clásica griega. Si las posiciones de las poleas cambian, la cadena entera se reorienta sola para adoptar de nuevo una forma catenaria.

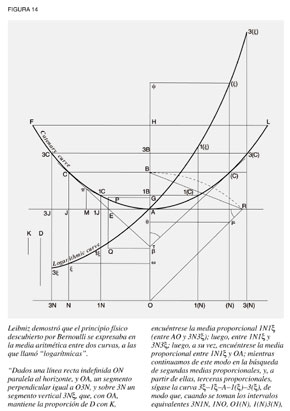
Aunque la Grecia antigua y Brunelleschi ya conocían esta característica, los principios subyacentes no se dominaron a cabalidad sino hasta que Godofredo Leibniz y Jean Bernoulli los descubrieron un siglo más tarde. Usando el cálculo de Leibniz, demostraron que la forma catenaria de la cadena era la forma que equilibraba la tensión física en cada punto de la misma (ver figura 13). Es más, Leibniz demostró que este principio físico correspondía a las funciones trascendentales elementales: la circular, la hiperbólica y la logarítmica (ver figura 14).

Regresa a nuestra comparación previa de la diferencia que hay entre las nociones geométricas abstractas de línea, área y volumen, y los requisitos físicos de la construcción de una columna, un arco y una cúpula. Tal como ya está implícito en el concepto de “poderes” desarrollado por Pitágoras, Arquitas, Platón, etc., incluso los conceptos geométricos de línea, área y volumen están determinados por la clase de principios físicos que, como Leibniz demostró, expresa la catenaria. La opinión aristotélica de que las líneas, las áreas y los volúmenes son entidades geométricas abstractas separadas de los principios físicos universales que las generan, es tan falsa como la fe en los poderes mágicos del panteón romano.

Brunelleschi usó una cadena suspendida para guiar el desarrollo de la curvatura de la cúpula en cada etapa de su construcción. A medida que se colocaba cada hilera de ladrillos, una cadena colgaba entre los nervios intermedios para guiar la curvatura. Así, la forma general de la cúpula la determinaba, no una curvatura definida por las matemáticas abstractas, sino un principio definido en términos físicos. Del mismo modo que una cadena suspendida se sostiene a sí misma de conjunto y en cada una de sus partes, la cúpula, cuya curvatura la guiaba la curvatura de la cadena suspendida, es una superficie que también se autosostiene de conjunto y en cada una de sus partes.

Aquí hago una advertencia a aquéllos aristotélicos que exigen “ver” la forma física de la catenaria en la figura final de la cúpula. Aunque Brunelleschi usó una forma del principio de acción mínima que Leibniz y Bernoulli descubrieron después, los rasgos de la cúpula no adoptan la forma de una cadena suspendida. Más bien, es el principio de acción mínima expresado en la cadena suspendida, del modo que ese principio se desarrolló después en la teoría de superficies de Gauss, en la teoría de multiplicidades de Riemann y en los principios de la economía física de LaRouche, el que le dio su forma a la cúpula. En “Believing Is Not Necessarily Knowing” (Creer no necesariamente implica saber)[1] LaRouche explica su descubrimiento:

“Podemos ilustrar esta conexión de forma apropiada con un caso que seguido he mencionado, desde 1988: la lección que debemos aprender de la exitosa construcción de Brunelleschi de la famosa cúpula de la Catedral de Santa María de Fiore, en Florencia. Y sigo remarcando ese ejemplo, no sólo porque logré redescubrir en 1987–88 un principio que Brunelleschi usó, a sabiendas de que tendría éxito, en efectuar un proceso de construcción que se creía físicamente imposible. El principio que usó para asegurar ese éxito fue el mismo principio de la catenaria que Leibniz, más de dos siglos después, identificó por primera vez como la expresión del principio universal de la acción física mínima.[FIGURE 14] Aquí, el arte y la ciencia se convirtieron en el mismo principio. El proceso ‘imposible’ de construcción realizado fue una demostración del principio de la verdad, que también se expresó como tal en el triunfo de la ciencia y el arte cristiano platónico sobre la tradición y los símbolos panteónicos falsos del romanticismo latino.

“El principio de acción mínima de Leibniz, el cual es la base de su descubrimiento de los logaritmos naturales, se expresa en la función catenaria, que es la curva física de ‘la cadena suspendida’ creada por una acción física. La escultura griega clásica prerromana reflejó esta curva como el principio del movimiento continuo capturado a medio movimiento, del modo que John Keats nos muestra esta equivalencia entre la verdad y la belleza en su ‘Oda a una urna griega’.

“De nuevo, ¡la verdad es un asunto de método! En este caso, la verdad de la cúpula como método de arte, y la verdad de la cúpula como método singular de un principio físico en su construcción exitosa, coinciden. Para lograr esculpir una figura capturada a medio movimiento, la mente del escultor tiene que sentir el impacto de lo que Leibniz definió como un principio físico de acción mínima universal, tanto como Brunelleschi confió en el uso de la catenaria en la forma de una cadena suspendida (una forma de materia en movimiento aun cuando parece estar inmóvil), que dio pie al proceso de construcción de la doble pared de la cúpula. El meollo no estribaba en que la cúpula terminada reflejara la forma catenaria, sino en que la capacidad de construir esas paredes dependía del principio de acción expresado en todas y cada una de las fases del proceso de construcción de la cúpula aun por terminar”.

La belleza de la cúpula demuestra lo veraz del descubrimiento de Brunelleschi. Sin embargo, se necesitarían los descubrimientos de Kepler, Fermat, Leibniz, Gauss, Riemann y LaRouche para comprender a cabalidad el principio subyacente.

El desarrollo de la idea física de la forma

El éxito de la construcción de la cúpula de Brunelleschi demostró que los principios arquitectónicos de la geometría física en los que se basaba eran universales. Esta perspectiva la expresó Johannes Kepler, quien 150 años después escribió, en Mystérium cosmográphicum, sobre la construcción del sistema solar.

“Percibimos la forma en que Dios, como uno de nuestros arquitectos, centró la tarea de construir el universo con orden y ejemplo, y colocó las partes individuales en la forma debida, como si lo que imitaba a la naturaleza no fuera arte, sino que Dios mismo había examinado el modo de construir al hombre que debía ser”.

Kepler, en esa obra, y luego en Nova astronomía y Harmonices mundi, descubrió que la forma del sistema solar, al igual que la de la cúpula, no estaba determinada por consideraciones matemáticas abstractas (que hubieran indicado órbitas perfectamente circulares), sino por principios armónicos físicamente determinados. Así, las órbitas planetarias elípticas, al igual que la cúpula de Brunelleschi, tenían el tamaño y la forma necesarios para poder expresar las relaciones armónicas de esos principios físicos.

Esta idea físicamente determinada dio otro paso en su desarrollo cuando Pierre de Fermat estableció que la forma de la trayectoria de la luz estaba determinada por el principio del tiempo mínimo, como lo expuso en su “Método de investigación del máximo y el mínimo”:

“Nuestra demostración se basa en un solo postulado, el de que la naturaleza obra a través de los métodos y senderos más fáciles y convenientes. Así, creemos que el postulado debería ser afirmado —y no como se hace de costumbre— al decir que la naturaleza siempre obra a través de las líneas más cortas. . . No buscamos los espacios o las líneas más cortas, sino aquéllas que pueden atravesarse con mayor facilidad, conveniencia y en el menor tiempo” (ver figura 15).

Leibniz, siguiendo los descubrimientos de Kepler y Fermat, generalizó estos descubrimientos en la forma de un principio de acción mínima universal en su Discurso de metafísica:

“El Arquitecto de todas las cosas creó la luz de tal forma que este resultado más bello nace de su misma naturaleza. Esa es la razón por la cual aquellos que rechazan la existencia de causas finales en la física, como Descartes, cometen un gran error, porque aparte de revelar las maravillas de la sabiduría divina, dichas causas finales nos hacen descubrir un principio muy bello, junto a las propiedades de cosas cuya naturaleza aún no percibimos con claridad, y que tenemos el poder de explicar y utilizar, de modo que podemos tener la facultad de explicarlas, junto con sus artefactos, tal como el Creador las usó para producir sus resultados, y para determinar sus fines. De esto debe comprenderse que las meditaciones de los antiguos sobre dichas cuestiones no deben tomarse a la ligera, como cierta gente piensa en la actualidad”.

De las trayectorias a las superficies

La cúpula de Brunelleschi muestra el camino hacia un desarrollo más elaborado del principio de acción mínima universal. Las órbitas planetarias, la trayectoria de la luz y las catenarias son todas trayectorias; es decir, curvas. La cúpula de Brunelleschi es una superficie de acción mínima.

Los conceptos necesarios para comprender las implicaciones de esta distinción los desarrolló Gauss, quien, remontándose a los descubrimientos de Kepler, Fermat y Leibniz (como hemos hecho nosotros), desarrolló los fundamentos de una teoría física de superficies.

El marco del descubrimiento de Gauss fue su medición de la superficie de la Tierra, la cual, por estar físicamente determinada, y en congruencia con el principio de Leibniz, tiene que ser una superficie de acción mínima. Por más de 20 años, Gauss hizo mediciones astronómicas y geodésicas de la Tierra. Las consideraciones de la geometría abstracta sugerirían que la Tierra es una esfera perfecta, ya que la esfera encierra el mayor volumen en la menor área. Pero como la Tierra es un cuerpo que rota en el sistema solar, su forma física no es esférica sino elipsoidal (ver figura 16). Sin embargo, las mediciones de Gauss determinaron una discrepancia entre la forma geométrica de una elipsoide y la forma física de la Tierra (ver figura 17).Esto lo llevó a descubrir que la forma física de la Tierra no era elipsoidal, sino algo más irregular. Gauss identificó la “forma geométrica de la Tierra, como esa forma que es perpendicular a la fuerza de gravedad por todas partes”. En otras palabras, Gauss, al igual que Leibniz antes con respecto a la catenaria, no trató de ajustar la Tierra a una forma sacada de los libros de texto de las matemáticas abstractas; más bien, inventó una nueva geometría que se amoldó a las características físicas de la Tierra en rotación.

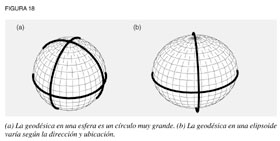
Gauss amplió este descubrimiento a una extensión del principio de acción mínima de Leibniz. Para Gauss, todas las superficies tenían una curvatura característica, la que a su vez, determinaba cierta trayectoria de acción mínima a la que denominó “geodésica”. Por ejemplo, en un plano, la geodésica es una línea recta, mientras que en una esfera, la geodésica es un gran círculo. En estos dos casos la curvatura es uniforme y, así, la geodésica es la misma en toda la superficie. En contraste, una elipsoide es una superficie de curvatura no uniforme. Por tanto, la geodésica difiere dependiendo de su dirección y posición sobre la superficie (ver figura 18).

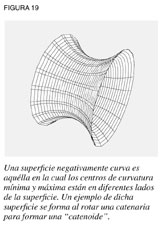
Para ilustrar esto, tienes que hacer algunos experimentos físicos. Toma un pedazo de papel, una esfera y una masa blanda de espagueti o algún otro objeto de forma irregular. Marca dos puntos en lugares diferentes sobre la superficie, y tiende un hilo entre ellos de forma que quede tenso. El hilo se amoldará de forma aproximada a la geodésica entre los dos puntos. Observa que en un plano la geodésica siempre es una línea recta, mientras que en la esfera siempre es un gran círculo, y en una masa de forma irregular la geodésica cambia de lugar en lugar y de dirección en dirección.

Existe otra distinción entre el plano y la esfera o la elipsoide. En el plano existe una cantidad infinita de trayectorias entre dos puntos cualquiera, pero sólo una de estas trayectorias es una geodésica, es decir, de acción mínima. Esto también ocurre en una esfera o elipsoide, excepto en el caso de que los dos puntos sean los polos; entonces, existe una cantidad infinita de geodésicas entre los dos puntos. La naturaleza limitada de la esfera y de la elipsoide produce una singularidad respecto a la naturaleza de las geodésicas.

Gauss investigó los principios generales a través de los cuales la curvatura de la superficie determinaba la característica de la geodésica. En este debate, la determinación de un medio para medir la curvatura de la superficie en cualquier punto tiene una pertinencia inmediata. Para nuestros fines, basta ilustrar esto con una demostración física. Dibuja un círculo en la masa colocando una marca en un punto del hilo y haciéndola rotar mientras sostienes la otra punta del hilo en una posición fija. Todos los radios de este círculo son geodésicas en diferentes direcciones. Ahora examina la curvatura de cada geodésica: variarán en cada dirección. Habrá una geodésica que sea la menos curva (de curvatura mínima) y otra que sea la más curva (de curvatura máxima). Inténtalo de nuevo, pero en una superficie diferente, como por ejemplo una masa de nuez con forma de pesas para hacer ejercicio. Los extremos redondeadas de la masa de nuez tienen las mismas características que la masa de espagueti, en la que el centro de la curvatura se encuentra siempre dentro de la masa. Sin embargo, algo diferente sucede en medio de la masa. Aquí, el centro de la curvatura está, o dentro o fuera de la masa, dependiendo de la dirección de la geodésica. Gauss denominó a esta característica “curvatura negativa”, y es la característica de la curvatura que expresa una superficie formada, por ejemplo, en una catenaria rotada llamada “catenoide” (ver figura 19).

Gauss comprobó que en cualquier superficie, sin importar lo irregularmente curva que sea, ¡las geodésicas de curvatura máxima y mínima siempre formarán ángulos rectos entre sí!

Así, la curvatura de la superficie expresa un principio físico, que a su vez determina la geodésica o trayectoria de acción mínima a lo largo de esa superficie. En el caso de la cúpula de Brunelleschi, era la forma general físicamente determinada de la superficie de la cúpula la que determinaba las curvaturas características, en forma longitudinal, circunferencial y hacia adentro. No obstante, mientras estaba en construcción, la forma general (aun inconclusa) tenía que formarse con las pequeñas modificaciones en las curvaturas longitudinales, circunferenciales y hacia adentro. El uso de la cadena suspendida de Brunelleschi para guiar estos cambios de curvatura en lo pequeño expresa la congruencia entre el principio de la catenaria y las características de acción mínima de la cúpula.

De las superficies a las multiplicidades

A partir del descubrimiento de Gauss, Bernhard Riemann generalizó este concepto un poco más, a la idea de una geodésica dentro de una multiplicidad de principios físicos universales. Estas multiplicidades, que tienen más “dimensiones” que superficies, no pueden verse de forma directa, pero, al igual que las superficies, sus características pueden conocerese directamente por un cambio en la geodésica.

Por ejemplo, la luz en la reflexión y la refracción sigue una trayectoria en una superficie, pero cada clase de acción expresa una trayectoria diferente debido a que la multiplicidad física de la refracción implica un principio, al cambiar la velocidad de la luz, que no existe en la multiplicidad de la reflexión. La adición de este nuevo principio a la multiplicidad de acción modifica la geodésica. Y viceversa, cuando se mide un cambio en la geodésica, eso indica la presencia de un nuevo principio físico en la multiplicidad.

Riemann desarrolló los medios para representar estas multiplicidades superiores mediante funciones complejas, a las que en forma metafórica expresó en la forma de superficies. Por ejemplo, las órbitas planetarias en secciones cónicas y la catenaria son trayectorias de acción mínima respecto a la multiplicidad de la gravitación universal. Cada una representa una geodésica respecto a la multiplicidad de la gravitación universal. Sin embargo, esto nos plantea una paradoja: ¿por qué la multiplicidad de la gravitación universal expresa dos clases distintas de geodésicas, secciones cónicas para las órbitas planetarias y catenarias para las cadenas suspendidas? Cuando el principio de la catenaria se expresa como una función en el dominio complejo de Gauss y Riemann, las órbitas en secciones cónicas son consideradas como una geodésica dentro del principio superior que representa la catenaria (ver figura 20).

En las figuras se muestran ejemplos más generales (ver figura 21). Éstas ilustran cómo la misma acción, cuando tiene lugar en diferentes multiplicidades, varía por las características de la multiplicidad. Piensa en las redes ortogonales de cada figura como las geodésicas mínima y máxima de cada multiplicidad. En cada caso, la curva mantiene la misma orientación angular con respecto a estas geodésicas. Pero, como las geodésicas varían de multiplicidad a multiplicidad, la acción cambia. Así, un cambio en los principios que determinan la multiplicidad modifica las geodésicas, las cuales a su vez modifican toda acción en esa multiplicidad. Y viceversa, para efectuar un cambio en cualquier acción física, uno debe actuar para modificar las características de la multiplicidad en la que la acción ocurre.

Ahora mira la cúpula de Brunelleschi desde esta perspectiva. La cúpula es una superficie cuya geodésica, en principio, se amolda a la catenaria. En tanto superficie de acción mínima, expresa una geodésica con respecto al principio de gravitación universal. Respecto a la multiplicidad de la historia universal, la construcción de la cúpula representó la geodésica de esa cultura moribunda del Imperio Romano al Renacimiento de Oro del siglo 15.

En nuestro lugar actual en la multiplicidad de la historia universal, la creación de la “universidad de combate sobre ruedas” del movimiento de juventudes de LaRouche, y el convertir a LaRouche en Presidente de los Estados Unidos, es, para nosotros, nuestra cúpula de Brunelleschi, la geodésica que va de la Edad Media que hoy amenaza, a un nuevo Renacimiento sin fin.

Traducción de María Pía Cassettari.

[1] . Nora Hamerman y Claudio Rossi, “Brunelleschi’s Dome: The Apollo Project of the Golden Renaissance” (La cúpula de Brunelleschi: el Proyecto Apolo del Renacimiento de Oro), en 21st Century, Science & Technology, edición de julio–agosto de 1989 (vol. 2, no. 4).

2. Íbid[.]

3. Lyndon H. LaRouche, “Believing Is Not Necessarily Knowing̶[1] (Creer no necesariamente es saber), en Executive Intelligence Review del 17 de enero de 2003 (vol. 30, no. 2)..