¡Nuestro combate contra el empirismo!

Escapemos de la tragedia a través de la paradoja

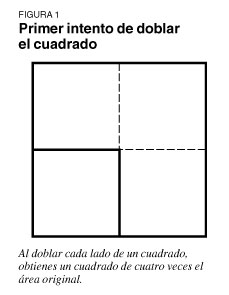
Nosotros, los que integramos el Movimiento de Juventudes Larouchistas (MJL), trabamos combate con un viejo enemigo que destruye a los seres humanos, mata la creatividad y pone de rodillas a civilizaciones enteras. No, no es Terminator y la rebelión de las máquinas votantes"; es el empirismo y la destrucción total del poder en el sentido platónico del término, de las mentes a las que ha infectado. Para recuperar el poder de la humanidad para mejorar nuestro dominio en y sobre el universo, nos remontaremos al Renacimiento, pero primero a Grecia, a los diálogos de Platón.

Platón demuestra en su diálogo Menón que el conocimiento es reminiscencia, y propone un experimento para ilustrarlo. Sócrates llama a uno de los niños esclavos de Menón para su demostración, y le pide doblar el tamaño de un cuadrado que dibujó en la arena. La primera propuesta es doblar el largo de cada lado del cuadrado, pero, al intentarlo, el niño descubre que en realidad hizo un cuadrado cuatro veces más grande (ver figura 1).

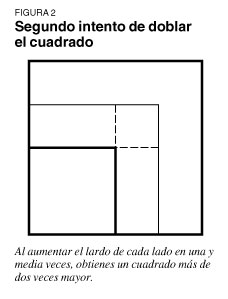
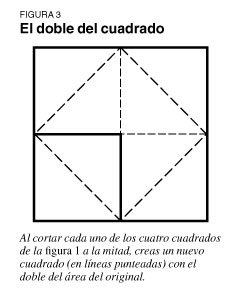
En un nuevo intento, el niño hace cada lado una y media veces más largo, lo que resulta en una figura que todavía es de más del doble del tamaño de la original (ver figura 2). Finalmente, regresando al cuadrado cuádruple, la idea de cortar cada uno de los cuatro cuadrados en mitades lleva a formar un cuadrado inclinado" en el centro, con cuatro triángulos, de los cuales el cuadrado original comprende dos; ¡así se dobla el cuadrado! (ver figura 3). El niño entiende el proceso y la validez del descubrimiento a través de las preguntas de Sócrates nada más; no hay ninguna afirmación o aseveración de hechos en lo absoluto.

Este descubrimiento es extraordinario en su demostración de las facultades cognoscitivas inherentes de cualquier ser humano (trata de hacerlo con extraños; ¡funciona!), y en las profundas implicaciones de lo que acabamos de descubrir. El diálogo Teetetes de Platón ahonda en el concepto de poder de una forma magnífica: el lado del cuadrado doble que acabamos de descubrir es inconmensurable con el lado del cuadrado original (ver Burn the Textbooks! Re-create the Original Discoveries" [Quema los libros de texto! Recrea los descubrimientos originales], en la edición de otoño de 2003 de 21st Century, pág. 8).

La imposibilidad de expresar la ``raíz cuadrada de 2" como un número de entre las fracciones infinitas que existen entre 1 y 2, expresa la noción de poder de Platón. Hemos generado algo que va más allá del infinito previo.

El verdadero poder es la capacidad de transformar todo el dominio de lo posible. Compara esto con la noción simple e infantil de poder en tanto ``más"; más caballos de fuerza en tu motor, más cafeína en tu bebida, más portatazas, más atractivo sexual, más decisiones, más alternativas, ¡mas tú! Es patente que estas nociones consumistas de poder son bestiales en sus implicaciones del potencial humano. En lugar del poder inmortal de transformar la trayectoria del progreso humano para mejorar nuestro dominio sobre la naturaleza, se degenera al poder para que signifique un control de las cosas ya existentes.

Luz y poder

Iluminemos nuestro verdadero concepto de poder, explorando la propagación de la luz. En la Grecia clásica se descubrió que la reflexión de la luz ocurría en una trayectoria de menor distancia. Esto puede demostrarse con un experimento que puedes hacer con ayuda de dos asistentes, una cuerda, un espejo y una linterna de mano.

Tú y un amigo se colocan en los extremos de un espejo que descansa sobre una mesa, al tiempo que enciendes la linterna (que colocas a la altura de tu ojo) dirigiéndola directo hacia el ojo de tu amigo sobre el espejo. Ahora, ambos sostengan la cuerda a la altura de sus ojos y hagan que la tercera persona ponga su dedo sobre el espejo en el lugar donde choca el rayo de luz (ver foto 1)

.iAhora la tercera persona puede divertirse un poco! Con la cuerda razonablemente tensa, que deslice su dedo en varias direcciones.¿Se le hace difícil mantenerla sobre el espejo? ¿Se levanta del espejo? Tu amigo siente que la cuerda se levanta cuando mueve su dedo porque la trayectoria que la luz siguió fue la de menor distancia; mover tu dedo a cualquier otra parte requiere aflojar la cuerda para que la cuerda siga tocando el espejo. ¡Increíble!

¿Cómo sabe" la luz cuál es el camino más corto? "Ay, hombre!" dice nuestro sombrío profesor de física: "La luz sólo rebota en el mismo ángulo en el que llegó. No hay una `menor distancia', es sólo un efecto de los ángulos iguales".

A lo mejor el profesor tiene razón; cuál es el problema? Seguiremos avanzando y descubriremos la importancia de este principio

Ahora veamos lo que pasa con la luz cuando entra al agua. Como habrás visto, cuando pones cosas en el agua los objetos sumergidos se doblan y quiebran en el paso del aire al agua. ¿Qué pasa aquí?

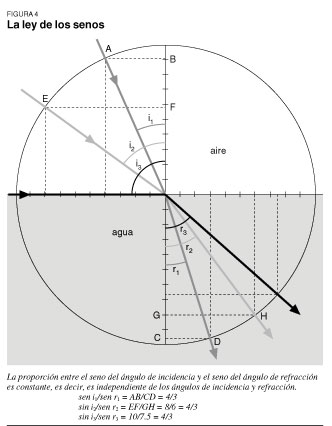
Usando el aparato del tanque de agua que aparece en la foto 2 podemos examinar la forma en que la trayectoria de la luz cambia cuando la apuntamos desde diferentes ángulos. Hemos doblado" la trayectoria de la luz. ¿Qué es lo que pasa? Abordaremos el problema desde dos perspectivas diferentes. Una es lo que hoy se enseña como la ley de Snell, que establece que los senos de los ángulos (las líneas horizontales en la (figura 4) son proporcionales según las diferentes velocidades de la luz en el aire y en el agua.

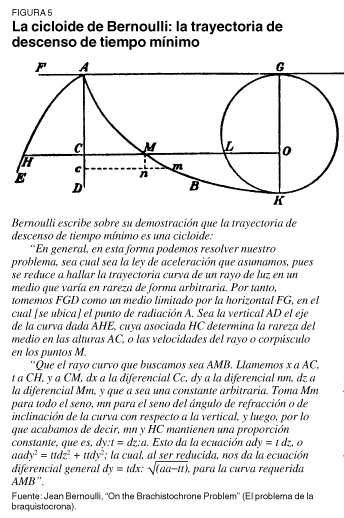
Esto describe el resultado que vemos. Pero, ¿explica por qué la luz sigue una trayectoria con esta relación? Mejor abordemos la pregunta desde la perspectiva de la intención. En el caso de la reflexión vimos que la luz siguió la trayectoria de la menor distancia. ¿Cuál es la intención ahora?

Toma el ejemplo de un salvavidas que rescata a un nadador que se ahoga. ¿Correría el salvavidas directo hacia el nadador, se zambulliría en el agua y nadaría directo hacia la víctima? Bueno, sólo si el salvavidas se graduó en física de una carrera universitaria de cuatro años. Un salvavidas caritativo correría por más tiempo sobre la playa a buena velocidad antes de saltar al agua y nadar el resto del trayecto. Fermat hipotetizó que nuestro humilde rayo de luz expresa el mismo sentido común:¡sigue la trayectoria del tiempo mínimo!

"¡Es absurdo!", brama el empirista, cómo podría la luz saber algo como eso? He leído a Bertrand Russell, el `propósito' es un concepto `científicamente' inútil. Esto es charlatanería! A la gente que piensa cosas como esa de seguro le parece valiosa la explicación mística de Kepler de las órbitas planetarias. Pero estas `armonías', o ideas como la del `tiempo mínimo', son consecuencia de las verdaderas leyes físicas determinísticas que gobiernan al universo".i

¿Sólo imaginamos que descubrimos principios ordenadores del universo? ¿Cómo podemos determinar si descubrimos una idea de mayor poder? ¡Ah, por supuesto que tratando de ampliar el dominio de lo que podemos hacer!!

El problema de la braquistocrona de Bernoulli

Cambiemos de ángulo por un momento, en tanto nos ocupamos del problema de la braquistocrona de Bernoulli que Leibniz planteó en su artículo de 1697, Acta eruditórum: "Problema mecánico geométrico de la curva de más rápido descenso: determinar la curva que une a dos puntos dados ubicados a diferentes distancias de la horizontal y no sobre la misma línea vertical, sobre la cual una partícula móvil que actúa por su propio peso inicia su movimiento desde el punto superior y desciende con mayor rapidez al punto inferior".

¦¿Cuál es la trayectoria más rápida en la que un objeto cae desde el punto A hasta el punto B?¿ Es una línea recta? ¿Un semicírculo? ¿Una parábola? O, ¿qué tal si resulta ser una curva generada de una forma completamente desconocida para nosotros? Este es un problema que no puede resolverse a partir de las matemáticas o la física empiristas. Así, entre la infinidad de curvas posibles, ¿cómo podemos determinar la mejor curva? ¿Qué tal si es físicamente creada de una forma que no puede expresarse (como lo fue la catenaria antes de Leibniz)? ¿Podría entonces plantearse como la solución a un problema propuesto en unas matemáticas en las que no puede expresarse? Por supuesto que no.

En lugar de asumir que la solución tiene que existir en una forma expresable, como hacen Leonhard Euler y Louis de Lagrange (ver El teorema fundamental del álgebra de Gauss de 1799, en www.21stcenturysciencetech.com/espanol.html o www.schillerinstitute.org/newspanish), y pregúntate en cambio: "¿Qué cosa generaría la solución?".

En lugar de observar las propiedades de bolas que caen, Bernoulli abordó este problema con principios. Al usar el principio del tiempo mínimo que gobierna a la luz, y la hipótesis de la luz en su viaje a través de una serie de densidades que cambian, Bernoulli desarrolló una diferencial, es decir, el principio que genera la curva, que da forma a su desenvolvimiento, y usó esto para demostrar que la braquistocrona (la trayectoria de tiempo mínimo) es, al igual que la tautocrona de Huygens (la trayectoria de igual tiempo), una cicloide. ¡Es increíble! Estamos usando la luz para determinar la trayectoria de un cuerpo que cae atraido por la gravitación (ver figura 5).

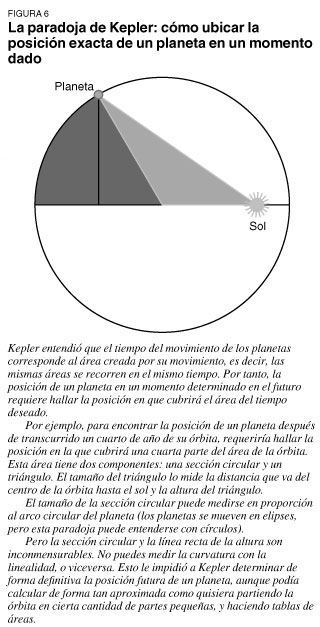
Bernoulli usa la siguiente idea física: si ordenáramos capas de diferentes medios una encima de la otra, arreglándolas de modo que la velocidad de la luz que viaja a través de ellas aumente en las capas inferiores, del mismo modo que la velocidad de un objeto en caída libre aumenta conforme a la distancia desde la que ha caído, entonces la luz que viaja a través de las capas seguirá (puesto que es luz) la trayectoria de tiempo mínimo, y el ordenamiento es tal que es el tiempo mínimo de algo que cae por la gravedad.

Bernoulli demostró que esta curva es la cicloide, la cual se genera trazando la posición de un punto sobre la circunferencia de un círculo que rueda a lo largo de una línea. Bernoulli escribe: ``Así, de un solo golpe, resolví dos problemas notables, uno óptico y el otro mecánico, y logré más de lo que otros me pedían; he demostrado que los dos problemas, que vienen de campos enteramente distintos de las matemáticas son, no obstante, de la misma naturaleza".(1)

Ahí donde la ley de Snell nos permite predecir la refracción de la luz (un proceso que pudimos recrear), el tiempo mínimo aumentó nuestro poder (dúnamis, en términos de Platón) ampliando el dominio del entendimiento humano para resolver paradojas.

La solución de Bernoulli al problema de la braquistocrona aprovechó el cálculo infinitesimal desarrollado por Leibniz, y esto también vino de la luz. A partir del principio de Fermat del tiempo mínimo, Leibniz desarrolló el principio general de la acción mínima universal, un concepto que revolucionó todo, incluso la física matemática.

Si todos los procesos del universo ocurren conforme a un principio de acción mínima universal, ¿qué implica esto sobre la geometría y la física? Bueno, significa que todo ocurre mediante principios únicamente, además del hecho de que la acción mínima sí existe. Esto significa que no puede permitirse ninguna consideración geométrica abstracta (por ejemplo, las formas en tanto formas), sólo acciones determinadas por los principios que gobiernan el universo.

¡Ajá! Escucha uno en la mente, aquí entra la introducción del tema de la disertación de habilitación de Riemann: "El espacio constituye un caso particular de una magnitud triplemente extendida. Una secuela necesaria de esto es que las proposiciones de la geometría no pueden derivarse de conceptos generales de cantidad, sino que esas propiedades que distinguen al espacio de otras magnitudes triplemente extendidas que puedan concebirse sólo pueden acumularse con la experiencia".

La necesidad de la polémica disertación de Riemann vino de la separación milenaria de la geometría, en tanto abstracción, que existe de manera independiente del universo físico. La paradoja que impulsó a Leibniz a desarrollar su cálculo surgió cuando al principio físico activo de la gravitación de Kepler se le impuso la estéril geometría abstracta, lo que a su vez dio lugar a la famosa paradoja de Kepler.

Cuando una idea de orden superior se proyecta o expresa en un dominio inferior en el cual es inexpresable, aparece en una forma paradójica. Piensa en los problemas de la inteligencia artificial. La paradoja de tratar de programar una mente artificial mecánica consiste en que el producto fundamental de la mente, las hipótesis, no puede derivarse de nada que haya existido previamente y no puede generarse de forma mecánica.

La paradoja era que, con la determinación de Kepler del tiempo que miden las áreas, se hizo posible, dadas dos posiciones de un planeta, medir el área y, así, el tiempo entre dichas posiciones. Pero era imposible hacer lo contrario; la ubicación exacta de un planeta en un momento dado en el futuro era imposible de determinar. El área implica tanto un arco circular (la medida de la porción de la sección circular) y una línea recta (el seno, que es la medida del triángulo), dos magnitudes que Cusa demostró son inconmensurables (ver figura 6).

La paradoja a la que Kepler llegó indica que no obtuvo una respuesta, aunque al mismo tiempo sí. La inconmensurabilidad sin resolver a la que uno llega cuando trata de determinar una posición en un momento dado es la respuesta. Es la única forma en que el universo, hablando a través de ese sistema matemático (el sensórium), podía responder a tu pregunta. Un poeta que trasmite con pasión una idea profunda no puede hacerlo de manera directa, sino sólo mediante la metáfora. Cuando LaRouche responde a tus preguntas en una forma que parece no responderlas para nada, la verdadera substancia de la respuesta la representan precisamente esas preguntas que nacen en tu mente.

Aquí, la substancia de la respuesta del universo a Kepler era un reto, al cual Leibniz respondió con unas matemáticas de un poder superior basadas en principios: su cálculo. Su concepto era determinar el principio del desarrollo de la diferencial (gravitación), para determinar la integral (órbita) de una forma en que pudiera generar, de forma cognocible, la ubicación deseada.

La respuesta de Leibniz a la respuesta del universo a Kepler era otra pregunta; Leibniz no sólo logró resolver el problema de Kepler, sino que su trabajo sentó las bases y planteó las preguntas a responder para los avances posteriores de Gauss y otros en el dominio complejo.

Principios invisibles

El desarrollo de los conceptos de acción mínima universal y del cálculo infinitesimal apunta a principios metafísicos muy superiores a los que el lenguaje de la geometría o la física pueden expresar. La implicación de la hipótesis de la hipótesis superior de un principio de acción mínima universal es la comprensibilidad cabal de un universo que existe como el desenvolvimiento de principios físicos, más que de una colección de datos sensoriales.

Tienes que buscar los principios invisibles, no los efectos. Un principio no existe en las propiedades de la materia, sino siempre en su relación con otros objetos, la relación primaria e inmediata entre el particular y lo universal subsume y es la sustancia de todas las relaciones con otros objetos".(2)

Es tu universo, responsabilízate por él. La economía está en bancarrota, tu universidad está perdiendo dinero, el entretenimiento popular es cruel y un hombrebestia fascista controla al Presidente de los Estados Unidos. ¿Qué crees que el universo está tratando de decirte?

(1.) Jean Bernoulli, On the Brachistochrone Problem" (El problema de la braquistocrona), en David Eugene Smith, A Sourcebook in Mathematics (Nueva York: Dover Publications, 1959), pág. 652.902. Lyndon H. LaRouche, Project A" (Proyecto A)

(2)The Science of Christian Economy (La ciencia de la economía cristiana, en la versión en inglés) (Washington, D.C.: Schiller Institute, 1991).Resumen/serads/Christian Economy Ad/christian.25SER,0,0,0,-1,0,,,2