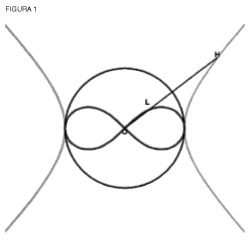
Las funciones Abelianas:
la diferencia entre el hombre y la bestia


Integrantes del Movimiento de Juventudes Larouchistas investigan
el principio de Acción mínima que gobierna la forma de una
burbuja de jabón dentro de un cubo, en una escuela de cuadros
en la Costa Este de los EU.

Todos los aristotélicos son unos mentirosos. De hecho, tienen que mentir, para mantener su creencia de que sus mentes son envases vacíos, indiferentes a lo que se ponga en ellas. Ellos proyectan esta visión de sí mismos en el universo, el cual, insisten, debe adecuarse a su visión degradada del hombre, al que consideran una caja vacía desprovista de principios, y sujeta a un orden que no puede conocer. Desprovisto de principios internos y externos, ninguna afirmación, a los ojos de tales aristotélicos, puede ser verdadera, sino sólo congruente en un marco lógico deductivo que descansa, no en principios universales, sino en alguna autoridad arbitraria que determina un conjunto de axiomas, postulados y definiciones.
Leibniz planteó este asunto en el prefacio de su Nuevo tratado sobre el entendimiento humano, el cual escribió en respuesta a los Ensayos sobre el entendimiento humano del promotor de la idea del hombre-bestia, John Locke:

"Las diferencias que nos separan no son, en verdad, de poca monta. Se trata de averiguar si, como piensan Aristóteles y el autor del tratado, el alma está en sí y por sí absolutamente vacía como un papel en el cual no se ha escrito nada (tábula rasa), y de si todo lo que en ella se graba procede de los sentidos y de la experiencia, o si, por el contrario, el alma contiente originariamente las razones iniciales de diferentes conceptos y doctrinas, que sólo con ocasión de los objetos exteriores se despiertan en ella, como yo lo creo, con Platón y con los escolásticos y con todos aquellos que interpretan el pasaje de San Pablo (Romanos 2:15) de que la ley de Dios está escrita en los corazones''.^[1]

En la doctrina de Aristóteles y Locke, el hombre no es diferente de una bestia, asunto que Leibniz también abordó en su Nuevo tratado sobre el entendimiento humano:

``Precisamente en esto se distinguen también los conocimientos del hombre de los del animal. Los animales se atienen únicamente a la experiencia y se gobiernan exclusivamente por los ejemplos; pues en tanto podemos nosostros juzgar, nunca pueden llegar a proposiciones necesarias mientras que los hombres son capaces de formar ciencias demostrativas. La facultad del animal, de sacar consecuencias, es por consiguiente algo distinto de la razón humana. Las consecuencias que sacan los animales son del mismo género que las de los meros empíricos, que afirman que lo que una vez ha sucedido sucederá también en otros casos aparentemente análogos, sin que sepan discernir si se dan las mismas causas. De aquí procede que les sea tan fácil a los hombres hacer cautivos a los animales y que los simples empíricos cometan tantos errores. Aun aquellas gentes que por la edad y la experiencia han contraído ciertos hábitos rutinarios, no están libres de estos errores cuando se abandonan a la experiencia, como lo podemos comprobar tanto en los negocios civiles como en los militares. No se toma bastante en consideración que el mundo cambia y los hombres se hacen más hábiles inventando nuevos expedientes, mientras que los ciervos y las liebres de los tiempos actuales no son más astutos que los de la antigüedad''^[2]

Hace poco, este autor, junto con varios miembros del Movimiento de Juventudes Larouchistas de los Estados Unidos y México, presenció en varias ocasiones una demostración pedagógica del conflicto arriba descrito. En respuesta a la distribución de los documentos de LaRouche, Cómo visualizar el dominio complejo y El culto pagano a Isaac Newton, en el marco de una presentación sobre el significado epistemológico e histórico de ataque de Gauss contra Leonhard Euler, Joseph Luois de Lagrange y Jean Le Rond d'Alembert en su prueba de 1799 de El teorema fundamental del álgebra, observamos que varios profesores y estudiantes de matemáticas reaccionaron con una defensa histérica de Isaac Newton y de Euler, e insistiendo que todo conocimiento tiene que expresarse en la forma de matemáticas lógicas deductivas. Observamos que estos individuos insistían que obvias falsedades históricas eran de hecho ciertas, sólo porque podían decirlas con gran energía. Tales objeciones, viniendo de aristotélicos, eran, por supuesto, mentiras disimuladas. No sólo defendían a sus amados ídolos Newton y Euler. Mas en lo fundamental, defendían su derecho a mentir a través de los métodos aristotélicos que Newton y Euler ejemplifican. La insistencia en una verdad conocible ``iba contra las reglas'' y garantizaba los arranques observados, de forma muy parecida a como un animal enfurecido defiende lo que percibe como los linderos de su territorio.

Con esto en mente, echa ahora un vistazo a la historia del desarrollo de lo que se conoce como ``funciones abelianas''.

Niels Henrik Abel

Hansteen fue un colaborador directo de Gauss, Alejandro de Humboldt, y Alexander Dallas Bache en la Unión Magnética, y fue responsable de tomar las mediciones magnéticas en todo el norte de Europa. Reconociendo el potencial de Abel, Holmboe y Hansteen consiguieron financiarle una gira por el continente para que pudiera interactuar con los pensadores más importantes de su época.

Después de una estancia en Berlín, Abel marchó a París, donde conoció a Augustín Cauchy -que era controlado por los jesuitas-, de quien dijo: "Ser un católico intolerante es algo raro en un hombre de ciencia''. Cauchy se ganó su reputación escribiendo disertaciones excesivamente largas sobre las manipulaciones formales de ecuaciones algebraicas y funciones complejas (qué en lo principal dirigió como un ataque contra la idea de Leibniz del infinitesimal), y se estableció él mismo como una suerte de insquisidor en la comunidad científica francesa.

Abel, quien ya había publicado numerosos descubrimientos revolucionarios, remitió una tratado titulado'"Informe sobre una propiedad general de una clase muy extensa de funciones trascendentales''a la Academia Francesa de Ciencias. Como la figura matemática principal de la Academia, se le confió a Cauchy el manuscrito

Molesto con el clima reaccionario de París, Abel partió hacia Viena, y de ahí de regresó a Noruega, donde, desprovisto de ingreso alguno, vivió en la pobreza, contrajo la tuberculosis, y murió a la edad de 26.

Entre tanto, el intolerante Cauchy se llevó el manuscrito de Abel a su casa y evitó que lo publicaran. Sólo en 1829, tras la muerte de Abel, cuando C.G.J. Jacobi supo de la biografía de Adrien Marie Legendre que escribió Abel, fue que su existencia salió a la luz. Tras leer una copia, Jacobi escribió:

"Qué descubrimiento éste del señor Abel. . . ¿Vióse jamás algo parecido? Pero como pudo ser que este descubrimiento, quizás el descubrimiento matemático más importante hecho en nuestro siglo, habiéndosele comunicado a nuestra Academia hace dos años, haya escapado a la atención de nuestros colegas".A pesar de la insistencia de Jacobi, Cauchy retuvo el manuscrito, permitiendo que lo publicaran sólo después de mucha presión en 1841, 15 años después de que fuera remitido, y 12 años después de la muerte de Abel.

El tema del descubrimiento de Abel aparece en la introducción de la biografía:

"Las funciones trascendentales hasta aquí consideradas por los matemáticos son muy pocas en número. Prácticamente toda la teoría de las funciones trascendentales se reduce a la de las funciones logarítmicas, y las funciones circulares y exponenciales, funciones que, en el fondo, forman una sola especie. Es sólo hasta hace poco que se empieza a considerar a algunas otras funciones. Entre éstas, las elípticas trascendentales, varias de cuyas notables y elegantes propiedades ha desarrollado el señor Legendre, tienen primacía. El autor ha considerado, en la biografía que tuvo el honor de presentar a la Academia, una clase muy amplia de funciones"

La historia de las funciones abelianas

Aunque el desarrollo de los transcendentales superiores de Abel y Riemann empieza propiamente con Johannes Kepler, es esencial reconocer los descubrimientos de Kepler desde la perspectiva del concepto pitagórico y platónico de poder, en tanto distinto del concepto aristotélico de energía.

Como Platón demuestra en sus diálogos Menón y Teetetes, los objetos en el dominio visible, tales como las líneas, los cuadrados y los cubos, los generan poderes que no pueden conocerse a través de los sentidos. No obstante, tales poderes son perfectamente conocibles a través del poder del número. La idea pitagórica-platónica de número en tanto proporción que significa un poder, es distinta de la idea aristotélica de un número que cuenta objetos del dominio visible.

Hablando de este mismo tema en sus Diálogos del idiota, Nicolás de Cusa distingue estos dos conceptos de número:

"Considero a los pitagóricos quienes, como dices, filosofan acerca de todas las cosas a través del número como filósofos serios y perspicaces. No es que piense que ellos pretendan hablar del número cual número matemático y cual número que procede de nuestra mente. (Pues es de suyo evidente que esta clase de números no es el comienzo de nada). Más bien, hablaban de forma simbólica y plausible sobre el número que procede de la Mente Divina del cual el número, un número matemático, es una imagen. Porque tal como nuestra mente es a la Mente Eterna e Infinita, así el número que procede de nuestra mente es al número que procede de la Mente Divina. Y le damos el nombre de "número" al número de la Mente Divina, igual que a la propia Mente Divina la llamamos por nuestra propia mente"

.Desde este punto de vista, reconocemos la existencia y las características de los poderes que generan las acciones que nosotros observamos, de las características de los números relacionados con las proporciones que esas acciones producen. Por ejemplo, el número asociado con doblar un cuadrado es un caso especial de una media geométrica entre dos extremos. En el caso particular del cuadrado el poder generador se expresa en la inconmensurabilidad entre su lado y su diagonal. Los aristotélicos ven esta clase de número como "irracional", porque es más complicado que las relaciones simples entre números enteros que expresan las proporciones lineares simples. Pero, para Cusa, esta inconmensurabilidad es en realidad más simple, porque indica la existencia de un poder superior:

"Más aun, de la relación del medio tono con el tono completo, y de la relación de la proporción de una mitad con una doble, siendo esta relación la que tiene el lado de un cuadrado con su diagonal, considero un número que es más simple de lo que la razón de nuestra mente pueda entender".

En términos más generales, el número asociado con la relación entre la diagonal de un cuadrado y su lado es un caso especial de toda una clase de magnitudes de una media geométrica entre dos extremos, la cual es una función de una clase de curvatura; a saber, de la rotación circular. Como Arquitas lo demostró en el caso de doblar el cubo, hay una clase aun superior de magnitudes de dos medias geométricas entre dos extremos, que genera una curvatura diferente; a saber, la acción cónica, del modo que lo ilustra su construcción del toro, el cilindro y el cono.

Luego, Cusa demostró que a todas estas clases de números, que Leibniz después llamaría "algebraicos", las subsume una clase superior de números, a los que Leibniz llamó trascendentales. Más aun, Cusa indicó que la generación de esta clase de números la gobierna la sucesión de descubrimientos de nuevos principios físicos:

"De forma parecida, la demostración de la inmortalidad de la mente puede buscarse de forma adecuada considerando el número. Puesto que la mete es un número vivo, es decir, un número que numera, y ya que cada número es, en sí mismo, incorruptible (aunque el número parece variable cuando se le considera en la materia, que es variable), no puede concebirse que el número de nuestra mente sea corruptible. ¿Cómo, entonces, pudo el autor del número (la mente) aparecer como corruptible?"

Partiendo de la perspectiva epistemológica de Cusa, Kepler demostró que el movimiento de las órbitas elípticas individuales de los planetas lo gobierna un principio universal que no puede expresarse con los números relacionados con la acción circular simple. Para resolver este problema, Kepler exigió el desarrollo de una nueva matemática

Esa matemática la proporcionó el cálculo infinitesimal de Leibniz, el cual, cuando se aplicó al problema de la catenaria, demostró que las funciones circulares y las logarítmico-exponenciales estaban unidas por el principio de acción mínima que expresa la catenaria. Esta relación unificada apuntó al descubrimiento de lo que Gauss luego llamaría el dominio complejo.

Pero, cuando el cálculo de Leibniz se aplicó directamente a las órbitas elípticas, surgió una paradoja. Esta paradoja no era matemática, más bien indicó la existencia de un nuevo principio físico que sólo podía caracterizarlo una nueva clase de número, hasta la fecha, sin descubrir

Kepler ya había anticipado la existencia de esta clase superior de trascendental en su investigación de las implicaciones de las secciones cónicas para la óptica. Aquí, Kepler reconoció que todas las secciones cónicas podían generarse mediante una función continua. Él expresó esa función con el movimiento de los focos de la sección cónica. Pensando en un círculo como si fuera una elipse en la que ambos focos son coincidentes, las otras secciones cónicas se generan por el movimiento de uno de los focos. Kepler notó la existencia de una discontinuidad entre la elipse y la hipérbola, una discontinuidad mediada por la parábola, la cual Kepler dijo tenía "un lado hacia lo curvo y el otro hacia lo recto".
El descubrimiento de esta clase superior de función elíptica llamó la atención del joven Gauss en su investigación de la lemniscata. Como he discutido en otras oportunidades, la lemniscata expresa el principio unificador superior entre todas las secciones cónicas, del modo que lo ejemplifica su relación en tanto la inversión de una hipérbola en un círculo (ver figura 1).^[3]

Y, a partir de esta relación, Gauss entendió que la lemniscata era la expresión de una nueva clase de trascendental, que era superior a los trascendentales circulares y logarítmicos. Esta clase de transcendental, como las magnitudes algebraicas o las funciones circulares y logarítmicas, no podía expresarse de forma directa, sino sólo por inversión. En otras palabras, sólo podía conocerse como "aquello que expresa el poder que genera la característica de esta especie de acción".
Para alcanzar una comprensión intuitiva de la perspectiva de Gauss, piensa en la generación del círculo a partir de las funciones circulares. Esto requiere que la mente salga del dominio de la percepción sensorial y entre al de los principios. En cuanto al círculo, éste se caracteriza por el movimiento uniforme. Pero, las funciones circulares, es decir, el seno y el coseno, son no uniformes. Desde el dominio de la percepción sensorial, es más "cómodo" generar lo no uniforme a partir de lo uniforme. Pero, desde el dominio de los principios, es todo lo contrario. El movimiento no uniforme del seno y el coseno expresa el principio generador superior que produce lo que parece ser un movimiento uniforme. Como Cusa insistió, y Kepler demostró, el movimiento uniforme no existe en el universo físico. Es sólo un artefacto de la acción trascendental no uniforme

El método de Gauss de la división del círculo probó, desde el punto de vista del dominio complejo, esta dependencia que tiene el movimiento uniforme del no uniforme. Fue esta investigación del círculo la que Gauss vió como un caso especial de la elipse, el cual lo llevó a investigar la lemniscata, que a su vez inspiró más tarde al joven Abel

Una manera de ilustrar esta relación es la siguiente.
Un círculo puede generarse con el movimiento uniforme de un extremo de una línea de longitud fija (radio) que gira, mientras el otro extremo está fijo. Conforme al teorema de Pitágoras, la relación entre el coseno y el seno con el radio es proporcional a la raíz cuadrada de 1 menos el cuadrado (ver figura 2)

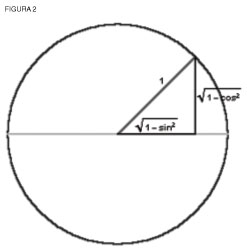
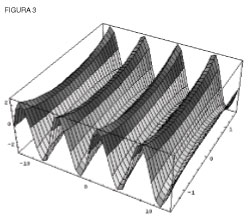
Un círculo también puede generarse variando la longitud de la línea móvil según sea el coseno (o el seno) del ángulo que hace con una línea fija. Al expresar la longitud de la línea móvil (coseno) en términos del seno, el arco del círculo varía de acuerdo a la raíz cuadrada de 1-seno 2

Sin embargo, cuando permitimos que la longitud de la línea móvil varíe por el coseno del doble del ángulo, producimos dos lemniscatas perpendiculares. Si variamos la longitud por la raíz cuadrada del doble del ángulo, generamos una lemniscata.

Si recordamos de ejercicios pedagógicos anteriores sobre el teorema fundamental del álgebra, al doblar el ángulo se cuadra el seno (ver "Volviendo visible lo invisible: El teorema fundamental del álgebra", en Resumen ejecutivo de la 1^a quincena de febrero de 2003, vol. XX, núm. 3). Así, si expresamos la longitud de la línea móvil en términos del seno, el arco de la lemniscata varía según la raíz cuadrada de 1 menos el cuadrado de un cuadrado, o la raíz cuadrada de 1-seno 4.

A partir de esta relación, Gauss reconoció que en el dominio complejo el principio que generó la lemniscata expresó una clase fundamentalmente diferente de relación que el principio que generó el círculo. En primer lugar, la función circular, aunque no uniforme, genera un movimiento uniforme. Pero, la función lemniscata genera un movimiento no uniforme. En el caso del círculo, el seno (o el coseno) es periódico. Por ejemplo, el seno varía de 0,1,0,-1,0 para cada rotación alrededor del círculo (ver figura 3).

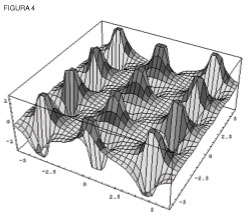
Pero, puesto que las funciones que generaron la lemniscata varían conforme el cuarto poder, estas funciones tienen dos períodos: 0,1,0,-1,0 y 0,i,0,-i,0 (donde i = la raíz cuadrada de -1. Ver figura 4).

Así, el poder que genera todas las secciones cónicas, del modo que las funciones lemniscáticas las expresan, es una clase superior de trascendental, que genera la acción no uniforme de la elipse mediante dos relaciones distintas pero conectadas.

Estas investigaciones tempranas de Gauss nunca se publicaron, y no se conocieron sino hasta que se descubrieron los cuadernos de notas de Gauss en los 1890. Pero, a partir del comentario intrigante que leyó en las Disquisitiones arithmeticae, el joven Abel reconstruyó por sí mismo el descubrimiento de Gauss, y luego fue aun más allá. Abel reconoció que la lemniscata, y las funciones elípticas relacionadas, sólo eran el primer paso de una "clase extensa de funciones trascendentales superiores". Así, las funciones circulares y logarítmicas no eran sino un caso especial de las elípticas, las cuales a su vez eran un caso especial de lo que desde entonces se conoce como funciones "Abelianas".

Pero, no se suponía que tales funciones existieran en el intolerante mundo animal del aristotélico Cauchy, así que él trató de ocultarlas con una mentira.

La verdad se impuso. Y allí, en parte, comienza la teoría de Riemann de las funciones abelianas.