El enfoque antieuclidiano de Kepler para abordar la astrofísica no versaba sobre los movimientos de los cuerpos celestes, sino sobre el poder que los causaba. Siluetas, figuras, formas y curvas; ninguna de ellas era apropiada para expresar un principio que provocara movimiento. Kepler prescinde de la perspectiva empirista de Ptolomeo, Copérnico y Brahe en la primera sección de su Nueva astronomía, demos trando que aunque sus tres sistemas parecen diferir, todos son geo métricamente equivalentes y, por ende, todos eran erróneos. Pues, ¿cómo puede la figura ser la causa de sí misma?

La adopción de Kepler de la metáfora al revivir el enfoque griego de la esférica, exigía algo que no es una forma, una curva, una figura ni ningún otro objeto geométrico expresado en términos sensopercep tuales: la gravitación. Al establecer su hipótesis de la gravitación universal y analizar sistemáticamente la manera en que opera esta idea (“especie”), llevó, de manera válida, el lenguaje geométrico inapropiado de su era más allá de sus límites, al borde de derrumbarlo.

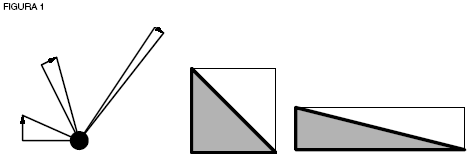
Kepler hipotetizó que los planetas se mueven en elipses a una velocidad inversamente proporcional a su distancia del Sol, debido a la fuerza debilitada de la gravitación a distancias más grandes (ver figura 1).

Surge un problema al aplicar esta idea: como la dirección de un planeta cambia a cada momento, ¿qué tan pequeños tienen que ser estos triángulos, y cuántos se necesitan para que representen una medición perfectamente precisa del tiempo? Si el triángulo tiene algún tamaño en lo absoluto, ¿no presupone la acción lineal en lo pequeño y elimina el cambio constante? Kepler transforma la idea de un número infinito de triángulos de movimiento, cada uno aparentemente tan pequeño como para no ser “nada”, en un área que va describiéndose de forma continua entre el planeta y el Sol, idea que Kepler usa como medida de tiempo (ver figura 2).

La distancia que recorre un planeta en un período determinado de tiempo es inversamente proporcional a su distancia del Sol. El mismo intervalo dado de tiempo genera triángulos con áreas iguales. Por ejemplo, a una distancia (radio) el doble de lejos del Sol, el movimiento por intervalo de tiempo (el cambio que muestran las flechas) es sólo la mitad de la distancia. Esto genera un triángulo del doble de la longitud, pero sólo la mitad de la altura, que, por tanto, representa la misma área. Esta área mide el tiempo.
FIGURA 2

Aquí, el planeta P ha recorrido una distancia del arco A desde el punto O, describiendo un área SPO, la cual es una medida del tiempo del movimiento. Esta área la conforman un sector circular CPO y un triángulo SCP. En tanto que el área de la sección circular CPO la mide la longitud del arco A, el área del triángulo SCP la mide h, el seno del arco A.

Como Cusa había demostrado más de un siglo antes, estas dos magnitudes, A y h, son inconmensurables. Dada una posición P, es posible medir y determinar el área encerrada, pero, dada un área deseada, ¿es posible determinar P con exactitud? Kepler encontró imposible esta tarea de determinar la posición exacta de un planeta en un momento futuro:

“Y en tanto que al primero [el sector circular] lo cuenta el arco de la excéntrica, al segundo [el triángulo] lo cuenta el seno de ese arco... Y las proporciones entre los arcos y sus senos son infinitas en número. Así, cuando comenzamos con la suma de ambos [el área buscada en tanto medición del tiempo], no podemos decir qué tan grande es el arco y qué tan grande es su seno, que corresponden a esta suma... Exhorto a los geómetras a resolverme este problema: ‘Dada el área de una parte de un semicírculo y un punto sobre el diámetro, encontrar el arco y el ángulo en ese punto, cuyos lados respectivos encierran el área dada’... Me basta creer que no puedo resolver esto a priori, debido a la heterogeneidad del arco en relación con el seno. Quienquiera que me demuestre mi error y señale el camino, será para mí el gran Apolonio”.

El “error” no es de Kepler, sino del lenguaje subdesarrollado que estaba empleando. Él había desarrollado un principio físico que yacía entre las “grietas” de la geometría, pero su lenguaje mate mático era de figuras, no de principios. Las grietas entre sus triángulos eran anomalías matemáticas, pero reflejaban una causa física siempre presente. Le correspondió a Leibniz introducir la metáfora (la dinámica) para crear una matemática física propia para abordar cuestiones físicas, más que meramente matemáticas.

El reto de Kepler para el futuro estimuló a Leibniz a dominar las “nadas”, tales como las grietas entre los triángulos de área de Kepler, en su descubrimiento original único de un cálculo de verdad infinitesimal (ver figura 3).

El cálculo de Leibniz no bastó. La doble inconmensurabilidad de la elipse rebasó los intentos de Leibniz de expresarla con funciones circulares. Habría que esperar a la obra de Gauss, Abel y Riemman, más de dos siglos después de Kepler, para una comprensión más cabal de las clases superiores de funciones trascendentales elípticas e hiperelípticas.

—Jason Ross.

—Traducción de Liza Niño, integrante del Movimiento de Juventudes Larouchistas en México.

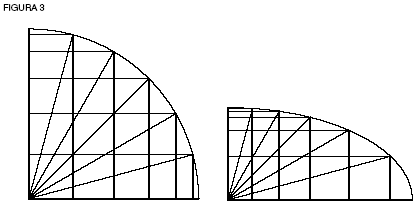Cuadrantes circulares y elípticos. La longitud de un arco sobre un círculo puede medirse directamente por el ángulo de rotación desde el centro, en tanto que la longitud de los senos (las líneas verticales) cambia de modo inconmensurable. Sobre la elipse, la inconmensurabilidad del seno sigue existiendo, lo mismo que otra: la longitud del arco ya no puede medirse por el ángulo (circular) de rotación desde el centro (¿cabe considerar siquiera la rotación sobre una elipse desde la perspectiva de la rotación circular constante?). ¿Puede una magnitud ser doblemente inconmensurable? De ser así, ¿qué la genera? Pues, ¿cómo podría un principio ya entendido generar algo incomprensible?