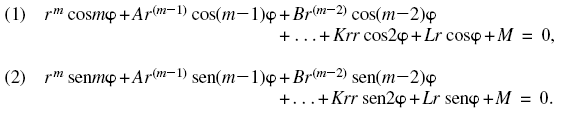
Recuadro 14: El enfoque geométrico de Gauss para abordar el álgebra
Lea El principio del ‘poder’ en formato PDF
Tal como Gauss expone de forma devastadora en su tesis doctoral de 1799, el planteamiento del álgebra como ontológicamente aritmética no logra explicarse: el álgebra no logra probar en términos propios lo que vino a conocerse como el teorema fundamental del álgebra.1
Para aclarar la cuestión, considera cómo Gauss describe a D’Alembert:
“Es correcto observar que D’Alembert aplicó consideraciones geométricas en la exposición de su prueba, y consideró a X como la abscisa y a x como la ordenada de una curva (según la costumbre de todos los matemáticos de la primera parte de este siglo para quienes la noción de las funciones era menos conocida). Pero todo su razonamiento, si uno sólo considera lo esencial, no descansa en principios geométricos, sino en los puramente analíticos, y una curva y una ordenada imaginarias son conceptos más bien difíciles y pueden ofender a un lector de nuestros tiempos. Por tanto, aquí he ofrecido más bien una forma de representación puramente analítica. He añadido este pie de página para que alguien que compare la prueba de D’Alembert con esta exposición concisa no recele de que se haya alterado nada esencial”.
Compara esto con la presentación de Gauss del dominio complejo ontológicamente geométrico.
Gauss comienza la parte de su tesis que se refiere a su propia demostración con dos lemas introductorios, donde introduce dos ecuaciones:
 |
Luego comienza su prueba propia mente dicha:
“El teorema en cuestión a menudo se prueba con la ayuda de números imaginarios, véase Euler, Introd. In Anal. Inf. T.I. pág. 110; considero que vale la pena mostrar cómo puede edicirse con facilidad sin su ayuda. Es bastante patente que para probar nuestro teorema no se ne cesita más que mostrar lo siguiente: al darse una función cualquiera X de la forma xm+Ax(m–1)+Bx(m–2)+ etc. +Lx+M entonces r y φ pueden determinarse de modo tal que las ecuaciones (1) y (2) sigan siendo válidas”.
No sólo afirma que no empleará números imaginarios, sino que ¡ni siquiera parece usar el álgebra! Estas ecuaciones (1) y (2) no involucran a x de ninguna manera, sino sólo a r y φ.
Para comprender cómo Gauss usa estas ecuaciones (1) y (2), abordemos de nuevo nuestra paradoja anterior, planteada en el recuadro 13 (ver figura 1).
| FIGURA 1 |
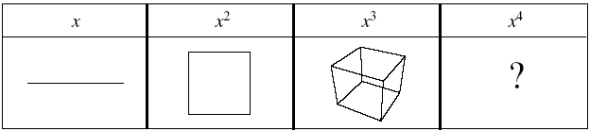 |
Tenemos líneas, cuadrados con una media y cubos con dos medias. ¿Qué forma podría corresponderle a una cantidad mayor de medias o a un número indeterminado de ellas? Lo que Jakob Bernoulli dio a conocer como su spira mirábilis (espiral maravillosa) (ver figura 2) nos da una pista.
 |
| La espiral logarítmica autosimilar de Bernoulli.2 La rotación de 90° al pasar de 1 a 2, repetida cuatro veces hasta los 360°, genera una longitud de 16, que es 24. |
Dicha espiral combina dos formas de acción, conocidas como la aritmética (simple, de adición repetida) y la geométrica (simple, de multiplicación repetida). La cantidad de cambio angular aritmético y aumento geométrico de la distancia se combinan en una acción: así, doblar la rotación cuadra la longitud multi pli cada, triplicar la cubica, y cuadruplicar nos da una comprensión geométrica de x4, x5, x6, y así sucesivamente, tan alto como quieras llegar.
La brecha infranqueable entre la acción lineal, cuadrada y cúbica, y el misterio de las formas de acción superiores, se ha resuelto al introducir una sola curva que, al multiplicar la cantidad de rotación, puede crear todas estas relaciones. De modo que la espiral equiangular trae lo que parecía infinito a lo finito, y abarca a una clase que antes de esto era desemejante, en una sola idea de acción a la que Leibniz denominó logarítmica.
Ahora bien, existen muchas espirales que podrían trazarse, espirales que crecen más o menos rápido. Interesémonos en los extremos: una línea recta (extensión pura sin rotación) y un círculo (rotación pura sin extensión) (ver figura 3).
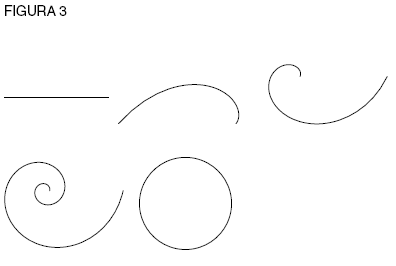 |
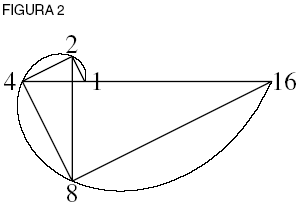
Inspecciona el círculo (ver figura 4). ¿Qué forma de número requiere? Llamemos a un lugar 1 y, naturalmente, a su opuesto –1.
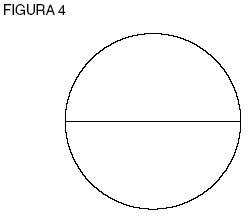 |
Nota que nuestra relación espiral previa sigue siendo válida: la rotación de 180° para llegar a –1, cuando se dobla a 360°, nos pone en 1, que es (–1)2. Pero, ¿qué hay de los otros lugares sobre el círculo? ¿A qué números corresponden? No pueden ser todos 1, ya que se trata de diferentes lugares (ver figura 5).
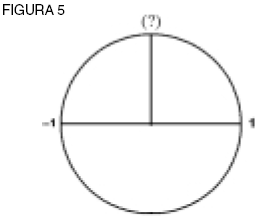 |
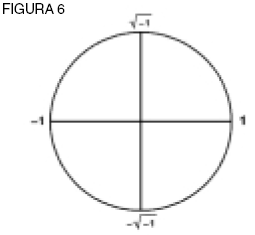 |
Manteniendo nuestro principio, (?)2 sería –1 por la propiedad logarítmica al doblar la rotación en nuestra espiral. Esto produce (?) = √–1, y su opuesto, –√– 1 (ver figura 6).
Los números “imaginarios”, aunque no existen en la línea númérica, sí existen y yacen por fuera de las anteojeras de los formalistas. Al extender estas acciones, creamos el dominio complejo.
“Supón, sin embargo, que los objetos son de una naturaleza tal que no pueden ordenarse en una sola serie, aun si fuera ilimitada en ambas direcciones, sino que sólo pueden ordenarse en una serie de series o, en otras palabras, formar una multiplicidad de dos dimensiones; si la relación de una serie con otra o la transición de una serie a otra ocurre de una manera similar, como lo describimos antes para la transición de un miembro de una serie a otro miembro de la misma serie, entonces, a fin de medir la transición de un miembro del sistema a otro, requeriremos, además de las unidades ya introducidas +1 y –1, dos unidades contrarias adicionales +i y – i. Claramente también tenemos que postular que la unidad i [√–1—Ndr.] siempre significa la transición de un miembro dado a un miembro determinado de la serie inmediatamente adyacente. De este modo, el sistema se ordenará doblemente en una serie de series”.3
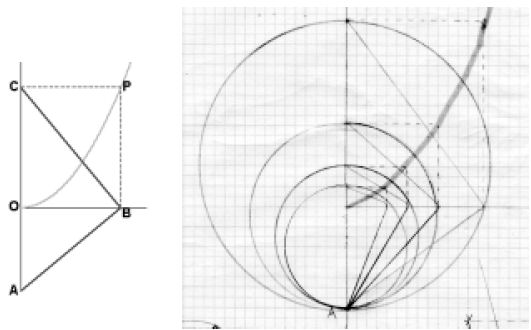
Ahora bien, ¿cómo podemos representar el cambio en este dominio complejo? Con números “normales”, la acción de cuadrar puede representarse como en la figura 7.
| FIGURA 7 | Las líneas trazadas desde A hasta el eje horizontal giran en ángulo recto para intersecar el eje vertical. La combinación de los puntos sobre los dos ejes forma una parábola. (Foto: cortesía de Mike Vander Nat). |
 |
Se puede considerar que cada uno de estos ángulos rectos combinados con el eje forma dos triángulos similares, produciendo la proporción A/X=X/Y (ver figura 8). Luego obtenemos AY/X = XY/Y, and AY/X=X, lo que nos da AY=X2. Entonces, cuando A=1, Y=X2 (ver figura 9).
| FIGURA 8 | |
 |
(Foto: cortesía de Mike Vander Nat). |
| FIGURA 9 | |
 |
|
La combinación de cierta cantidad de estos triángulos genera la parábola. (Foto: cortesía de Mike Vander Nat). |
|
Cada movimiento horizontal está “casado” con un cambio vertical de rela ción cuadrada con la horizontal. Su unión, la parábola, expresa el proceso de cuadrar.
Pero, ¿qué sucede si tomamos todo el campo complejo? Éste es un espacio bidimensional, y cada resultado del proceso de cuadrar también es bidimensional. ¡Juntos producen cuatro dimensiones! Con razón D’Alembert, “no descansa en principios geométricos, sino en los puramente analíticos”.
Gauss resolvió esto con la espiral logarítmica. Si cada acto de doblar la rotación cuadra la longitud, podríamos expresar cualquier lugar (a+b√–1) como r (cosφ+√–1 senφ) (ver figura 10).
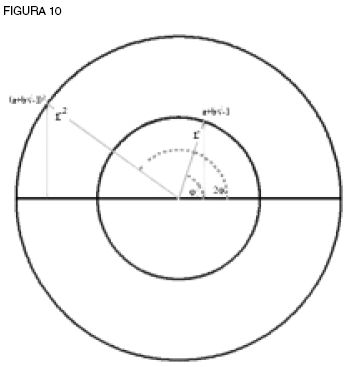 |
Y, al cuadrarla en espiral, obtenemos r2 (cos2φ+√–1 sen2φ).
¿Reconoces algo del documento de Gauss de 1799? Gauss simplemente aplica esta transformación a toda su ecuación algebraica X=xm + Ax(m–1) + Bx(m–2) + etc. + Lx + M=0, creando en cambio para cada x, r(cosφ+√–1 senφ) y produciendo:
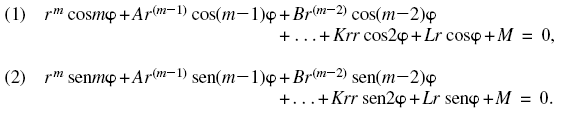 |
Esto mantiene separadas las partes con y sin 2 1, construyendo geométricamente dos superficies, donde D’Alembert sólo rumió falsamente una sola curva inexistente (ver figura 11).
| FIGURA 11 | |
 |
 |
| El MJL construyó en Filadelfia, EU un modelo geométrico que corresponde al teorema fundamental del álgebra de Gauss (der.). (Foto: Dan Sturman/EIRNS). | |
A partir de estos primeros pasos, Gauss, en su papel de 1799, logra usar con simplicidad y elegancia la naturaleza geométrica ontológicamente trascendental del número para demostrar una característica (el teorema fundamental) de su sombra, el álgebra. ¡Qué necios son aquéllos que pretenden explicar el universo imaginándose que sus sombras son la realidad!
—Jason Ross.
—Traducción de María Pía Cassettari.
[1]. ¿Cuánto tiempo, esfuerzo y dinero derrochan anualmente los estudiantes en su intento de explicar “la economía financiera” en base a la teoría monetaria? Quizás pudieran sacarle provecho a su tiempo contabilizando a cabalidad semejante desperdicio, por año.
[2]. “Volviendo visible lo invisible: El teorema fundamental del álgebra”, por Bruce Director (Resumen ejecutivo de la 1a quincena de febrero de 2003).
[3]. “La metafísica de los números complejos”, de Carl Gauss (Werke, vol. 2, págs. 171–178).
Para consultar el documento antedicho de Gauss y el trabajo del MJL con el documento de Gauss de 1799, visita http://www.wlym.com y www.wlym.com/~jross/gauss/.