Recuadro 1: Tres especies de número
Lea El principio del ‘poder’ en formato PDF
¡Hagamos un juego! Un jugador construirá geométricamente dos longitudes por el medio que elija. ¿Puede el otro jugador determinar siempre cómo fueron creadas las longitudes? De hecho, ¿podría en lo absoluto hacerlo? ¡Alo mejor éste no es un juego que valga la pena jugar!
Una primera hipótesis sería que el constructor tomó cierta longitud, y simplemente hizo dos líneas reproduciendo su longitud un número entero de veces: por ejemplo, usando — como nuestra unidad básica, podríamos construir longitudes sumando esta línea a sí misma, y crear quizás
— — —
y
— — — —
con la unidad. Estas dos líneas tienen lo que los pitagóricos llamaban una relación racional entre sí, expresada como la proporción de 4 a 5, 4:5 o la conocida fracción 4/5. Pero, ¿cómo podemos encontrar la unidad si las líneas no están marcadas de antemano? Un algoritmo que encontrará la línea común que generó a ambas (¡si es que existe alguno!), funciona midiendo la más larga con la más pequeña, y usando luego el residuo restante para tratar de medir la longitud original más pequeña:
Por ejemplo, de ser el segundo jugador y nos dieran las longitudes:
— — — — — — — — — — — y
— — — — — — —
Podríamos medir la más larga con la más pequeña:
— — — — — — — | — — — —
Lo que deja un pequeño residuo:
— — — —
El cual puede usarse para medir la línea
original más pequeña:
— — — — | — — —
Ahora la línea de la derecha también tiene un residuo:
— — —
Ahora, mide de nuevo, esta vez midiendo el residuo de la izquierda con el de la derecha:
— — — | —
Ahora tenemos un residuo a la izquierda que puede medir el de la derecha:
— | — | —
¡Ajá! Ahora ya se dio cuenta de todas las líneas y pueden expresarse, ya que pueden construirse a partir de la unidad de magnitud más pequeña. ¡Haz la prueba con un amigo!
Ahora bien, ¿será que esta técnica siempre funcionará? ¿Qué pasa si dos magnitudes no tienen una medida literal en común y nunca pudiéramos encontrar una unidad común?
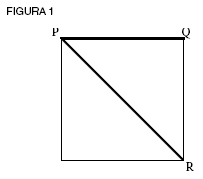
Toma el caso del lado de un cuadrado (PQ) y su diagonal (PR) (ver figura 1). Como indica el diálogo Menón de Platón, la diagonal es la solución para doblar el cuadrado, en tanto solución a un problema de área y no de longitud. Aquí, la diagonal no la creó la simple adición de líneas. La misma técnica exhaustiva antes aplicada
 |
 |
cobra una nueva forma geométrica con este ejemplo, que deberías de reproducir con un cuadrado de papel.
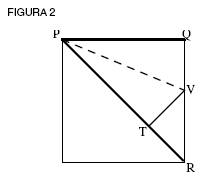
Dobla la línea superior PQ sobre la diagonal PR (ver figura 2). Q llegará a Ty tendrás un doblez PV sobre tu hoja. Observando PTR, esto es similar al método que usamos antes con las líneas. Cortamos la línea PT (de longitud PQ) de la hipotenusa PR, dejando un residuo TR. Pero ahora ha sucedido algo notable. Como TV (y TR) son iguales a QV en la construcción, y los lados de un cuadrado son iguales, QR–QV es lo mismo que PQ–TR, donde TR es el residuo PR–PQ. Esto es análogo a la medición previa de 7 con 4. Pero, ¡mira! El pequeño triángulo restante VTR conserva exactamente las mismas relaciones que el triángulo original PQR, de modo que ¡este proceso nunca terminará! ¿Qué implica esto? ¿Cuán pequeña es nuestra unidad más pequeña final, si existe en realidad?
¡Probemos de nuevo! ¿Qué tal si hubiéramos encontrado una unidad común? ¿Qué clase de proporción guardarían las dos longitudes? Bueno, si cada longitud está compuesta por un número de la unidad, entonces podría o no dividirse exactamente a la mitad produciendo unidades enteras (o es par o es impar). Luego, si PR fuera impar, entonces el cuadrado que genera lo conformaría un número impar de cuadritos unitarios, pero se suponía que PR formara un cuadrado del doble de grande que PQ, y es obvio que un número impar no es el doble de grande que nada, pues impar significa que ¡no puede dividírsele en dos partes iguales (ver figura 3)!
 |
Un cuadrado cuyos lados son impares puede pensarse como un cuadrado par al que se le añadió una escuadra en forma de “L”. Esa escuadra está conformada por dos líneas pares, y resta un pequeño cuadrado. El cuadrado restante si gnifica que todo el cuadrado con lados impares tiene un número impar de unidades de área. |
De modo que, PR tiene que ser par para que sea el doble del cuadrado PQ. Ahora bien, si PQ también fuera par, significaría que se nos fue la mano al construir nuestra pequeña unidad, pues una proporción de dos números pares también es una proporción con un número impar. Por ejemplo, la proporción de 2 a 3 podría ser de 4 a 6 si de veras quisieras llamarla así, tal como un medio es lo mismo que dos cuartos. La única conclusión que queda es que PR es par, en tanto que PQ es impar, lo cual hace que el cuadrado PQ también tenga un número impar de pequeños cuadrados unitarios de área. Pero espera, PR es par, lo cual hace divisible de este modo al cuadrado PR (ver figura 4):
 |
La mitad del área de PR es par, pero el cuadrado PQ, que se supone que es la mitad del cuadrado PR, ¡es impar! Hemos fallado de nuevo, y ésa era la última posibilidad. ¿Qué significa esto? ¿De veras no hay ninguna posibilidad de una unidad común? Entonces, ¿cómo podemos expresar la relación entre estas longitudes?
Ésta es una relación irracional: el lado PQ y la diagonal PR de un cuadrado no pueden expresarse las dos como una proporción que pueda contarse con una unidad común. Pero la incapacidad para expresar una magnitud no significa que sea incognoscible ni que no pueda construirse.
Teetetes relata, en el diálogo Teetetes de Platón, su concepto de una clase entera de tales magnitudes: aquéllas que corresponden a los lados de cuadrados con áreas conmensurables, y a los lados de cubos con volúmenes conmensurables. No debiera sorprendernos que el poder para doblar un cuadrado o un cubo, al ser de un poder superior que el necesario para doblar la línea, sea inexpresable en términos de líneas.
La especie trascendental
Más allá de estas dos especies, la racional y la irracional, existe la trascendental. La exposición de Nicolás de Cusa de la cuadratura del círculo (la medición exacta de la circunferencia de un círculo en términos de su diámetro) demuestra esta imposibilidad (ver figura 5).
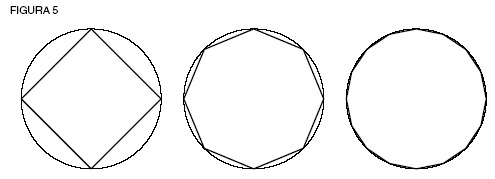 |
El intento de aproximarse a un círculo usando polígonos con cada vez más lados, falla. Incluso en un polígono con un número astronómico de lados, cada lado minúsculo sigue siendo recto, en tanto que el círculo es curvo en ese intervalo. El fracaso de este enfoque demuestra, de forma negativa, que el círculo es de una especie trascendental superior a la de las líneas de los polígonos con los que pretendemos alcanzarlo. Esto sólo puede captarse con un poder superior, al que Cusa llamó el principio isoperimétrico (del “mínimo y el máximo”).
El problema de Kepler, que surge como una distinción entre los irracionales y los trascendentales, era el encargo a futuros pensadores de crear una física matemática fundada en el poder como lo primario, más que en el fraude que hace caso omiso de la física y que sólo puede expresar los efectos de un poder mediante las imágenes de la estela que deja a su paso.
Las funciones de superficie de Riemann, como las elaboró en obras tales como su Teoría de las funciones abelianas, revelan a más cabalidad la implicación geométrica de la existencia de las funciones circulares, que son infinitamente poderosas desde la perspectiva de los irracionales algebraicos, y de formas de trascendentales de poderes aun mayores que los circulares.
—Jason Ross.
—Traducción de Betiana González,
integrante del Movimiento de
Juventudes Larouchistas.