(Versión imprimible) recuadro 3

La secuencia que representa los volúmenes de aquellos cubos que una persona puede construir con cubos unitarios, es 1, 8, 27, 64, etc. En el siglo 4 a.C., Platón desafió a sus colaboradores a resolver un viejo problema: construir un cubo de volumen 2. En otras palabras, a construir dos cubos, uno de los cuales pudiera contener exactamente el doble de material que el otro. Esto significa que tenemos que encontrar un cubo intermedio que no está en la secuencia de los cubos generados por cubos unitarios.

Hipócrates de Quíos había demostrado que puede llegarse a cada uno de los números cúbicos normales de la secuencia mediante un proceso de crecimiento geométrico, en el que dos pasos geométricos median el crecimiento de 1 al siguiente número cúbico más grande. Por ejemplo, 1, 2, 4 y 8 resultan del proceso de doblar; y 1, 3, 9 y 27 del de triplicar. Entre cada par de extremos (1 y 8, o 1 y 27) hay dos medias geométricas (2 y 4, o 3 y 9, respectivamente). Al ir doblando un cubo de 1 a 8, la longitud de las aristas crece de 1 a 2. Pero las dos medias geométricas entre 1 y 2 no han de encontrarse sobre una regla. De hecho, lo mejor que uno consigue con los cálculos actuales es una aproximación cercana.

Sin embargo, ¡Platón no pidió una aproximación cercana! Arquitas, un estrecho colaborador de Platón, descubrió la primera solución exacta al problema (ver figura 1). Arquitas sabía que su descubrimiento generaría un cubo doblado, porque resolvía el problema general que planteó Hipócrates. Por fortuna, contamos con una descripción de la construcción de Arquitas que podemos usar hoy para reproducir su viejo descubrimiento por el método de la esférica.

Como jóvenes que crecemos en el siglo 21, educados en universidades dirigidas por sesentiocheros, nos es fácil creer que Arquitas nunca construyó su modelo. Pero esto es sólo porque nos han lavado del cerebro para que desatendamos el proceso de producción en tanto actividad humana. La mayoría de los miembros del Movimiento de Juventudes Larouchistas ha construido artefactos que demuestran diferentes aspectos de las acciones en la construcción de Arquitas. La foto muestra a jóvenes del MJL en Los Ángeles usando su modelo de Arquitas en un taller didáctico.

No obstante, que sepamos, nadie ha construido aún en realidad un modelo completo del toro, el cilindro y el cono en el que los tres intersequen en el punto cúbico. La dificultad no radica en construir el cono o el cilindro, sino en la construcción del toro. No puedes envolver un toro con un pedazo de papel sin que se estire. Probamos con aros de madera, círculos de papel, resortes de juguete y gráficos computarizados, pero sólo ofrecen un armazón a revestir con una superficie mental (ver figura 2). Pero éstos no son toros reales. Quizás debamos seguir la recomendación media brusca de Eratóstenes: “No procures emprender la difícil empresa de los cilindros de Arquitas”.

FIGURA 1
	Representación gráfica computarizada de la construcción de Arquitas.
FIGURA 2
	Representación gráfica computarizada del toro.

Hace poco nos inspiró la lucha por salvar el sector automotriz estadounidense, y construimos una máquina– herramienta que incorpora dos niveles de acción circular, la cual talla una cavidad toroidal en algo de yeso a medio secar. La herramienta que diseñamos tiene una pila de discos compactos sujeta a un perno de 3/8 de pulgada, con otros tres discos compactos pegados de forma perpendicular a ranuras talladas en la pila de discos a distancias iguales. A estos discos les pegamos semicírculos de cartón del tamaño del radio que queremos que tenga nuestro toro.

Luego, mientras va secándose el yeso en un recipiente, usamos un taladro para calar un medio toro (ver figura 3). Entonces pudimos usar esto de molde para crear toros positivos, a uno de los cuales lo fabricamos con la muesca de una sección cilíndrica.
La intersección de las acciones que generan al toro y al cilindro nos da una curva especial que se extiende desde el centro del toro hasta el extremo opuesto del mismo, a la que Eudemo llamó la curva alabeada (ver figura 4).

FIGURA 3

Máquina–herramienta para construir toros y su producto.

FIGURA 4

La curva alabeada como una intersección del toro con el cilindro.

Ahora bien, el recorrido de una acción cónica particular interseca esta curva alabeada en un punto que, al conectarla al centro del toro con una línea, produce una longitud igual a la mayor de las dos medias geométricas deseadas (ver figura 5).

Al proyectar esa intersección directamente hacia abajo, a un plano que rebana al toro a la mitad (como si fuera una dona), uno obtiene un segundo punto que, al conectarse al centro del toro con una línea, genera la media más pequeña (ver figura 6). Si ambos extremos, el radio y el diámetro de la base del cilindro, son 1 y 2, respectivamente, las medias más corta y más larga te darán la longitud de las aristas respectivas del cubo doblado y del cuadruplicado.

FIGURA 5

La intersección del cono con la curva alabeada genera la mayor de dos med ias geométricas entre 1 y 2.

FIGURA 6

La proyección hacia abajo de la intersección del cono con la curva alabeada genera la menor de dos medias entre 1 y 2.

Ahora veamos de nuevo el problema. Queríamos las medias para construir un cubo doblado, y terminamos con una construcción, usando superficies de revolución, para encontrar un conjunto de líneas rectas (ver figura 7).

FIGURA 7

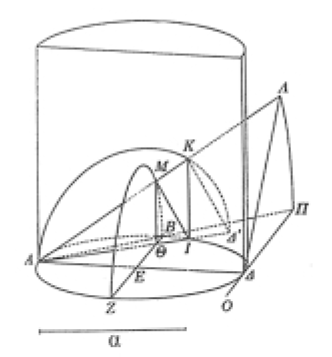Diagrama de Eudemo de la construcción de Arquitas. ¡Las intersecciones de las superficies producen líneas rectas, no volúmenes!

¿No es extraño? Los volúmenes que contienen las superficies dependen de un principio diferente que el del volumen del cubo. Empero, es la intersección de estas superficies la que nos da las medias para doblar el cubo. Estamos usando dos órdenes de magnitud inferiores para generar una magnitud de orden superior. Es como usar la combinación correcta de chuletas de cerdo para construir un filete de res, o como encontrar la combinación correcta de delfines y chimpancés que produce un ser humano. Sin embargo, ¡aquí estamos usando líneas y superficies para construir un volumen! Esto no sólo es extraño, sino paradójico.

Pensemos como Arquitas —quien concibió sus ideas de las medias proporcionales al investigar la música— e invirtamos la construcción. Tal vez el ordenamiento de las tres acciones circulares se determine de arriba para abajo, más que de abajo para arriba. En este caso, el punto de intersección no lo genera el agregado de tres superficies, tal como un intervalo musical no es una nota más otra. Más bien, Arquitas las ordenó para que reflejaran un proceso que no es continuo en el dominio visible. Imagina un cubo que crece de forma continua hasta alcanzar ocho veces su volumen, pasando por el doble del mismo. El ordenamiento de Arquitas de las acciones capta así dos instantes, el del cubo doblado y el cuadruplicado, y los trae del proceso continuo invisible al dominio de lo visible.

El toro, el cilindro y el cono son las huellas que deja este acto de volver visible lo invisible. También lo es la esfera, que también es una superficie generada por dos acciones circulares ortogonales. De modo que, la construcción de las dos medias entre dos extremos cualquiera puede representarse sobre la esfera. Pero la esfera carece de la capacidad de generar esas medias por sí misma. La construcción de las medias requiere que el hombre desenvuelva la acción esférica. En términos metafóricos, el descubrimiento de Arquitas y nuestra pequeña máquina–herramienta formaron las dos medias entre el dominio invisible del crecimiento cúbico continuo y el dominio visible.

—Peter Martinson.
—Traducción de Emiliano Andino,
miembro del Movimiento de Juventudes
Larouchistas en Argentina.

Estudios estratégicos